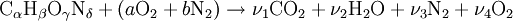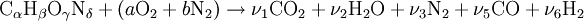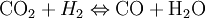To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Adiabatic flame temperature
In the study of combustion, there are two types of adiabatic flame temperature depending on how the process is completed: constant volume and constant pressure. The constant volume adiabatic flame temperature is the temperature that results from a complete combustion process that occurs without any work, heat transfer or changes in kinetic or potential energy. This is the maximum temperature that can be achieved for given reactants because any heat transfer from the reacting substances and/or any incomplete combustion would tend to lower the temperature of the products. The constant pressure adiabatic flame temperature is the temperature that results from a complete combustion process that occurs without any heat transfer or changes in kinetic or potential energy. Its temperature is lower than the constant volume process because some of the energy is utilized to change the volume of the system (i.e., generate work). Product highlight
Common Flames
In daily life, the vast majority of flames one encounters are those of organic compounds including wood, wax, fat, common plastics, propane, and gasoline. The constant-pressure adiabatic flame temperature of such substances in air is in a relatively-narrow range around 1950°C. This is because, in terms of stoichiometry, the combustion of an organic compound with n carbons involves breaking roughly 2n C–H bonds, n C–C bonds, and 1.5n O2 bonds to form roughly n CO2 molecules and n H2O molecules. Because most combustion processes that happen naturally occur in the open air, there is nothing that confines the gas to a particular volume like the cylinder in an engine. As a result, these substances will burn at a constant pressure allowing the gas to expand during the process. Common Flame TemperaturesAssuming initial atmospheric conditions (1 bar and 20°C), the following table list the adiabatic flame temperature for various gases under constant volume conditions. The temperatures mentioned here are for a stoichiometric fuel-oxidizer mixture (i.e. equivalence ratio φ = 1).
ThermodynamicsFrom the first law of thermodynamics for a closed reacting system we have,
where, RQP and RWP are the heat and work transferred during the process respectively, and UR and UP are the internal energy of the reactants and products respectively. In the constant volume adiabatic flame temperature case, the volume of the system is held constant hence there is no work occurring, and there is no heat transfer because the process is defined to be adiabatic: RQP = 0. As a result, the internal energy of the products is equal to the internal energy of the reactants: UP = UR. Because this is a closed system, the mass of the products and reactants is constant and the first law can be written on a mass basis,
In the constant pressure adiabatic flame temperature case, the pressure of the system is held constant which results in the following equation for the work, Again there is no heat transfer occurring because the process is defined to be adiabatic: RQP = 0. From the first law, we find that, Recalling the definition of enthalpy we recover: HP = HR. Because this is a closed system, the mass of the products and reactants is constant and the first law can be written on a mass basis,
We see that the adiabatic flame temperature of the constant pressure process is lower than that of the constant volume process. This is because some of the energy released during combustion goes into changing the volume of the control system. One analogy that is commonly made between the two processes is through combustion in an internal combustion engine. For the constant volume adiabatic process, combustion is thought to occur instantaneously when the piston reaches the top of its apex (Otto cycle or constant volume cycle). For the constant pressure adiabatic process, while combustion is occurring the piston is moving in order to keep the pressure constant (Diesel cycle or constant pressure cycle).
If we make the assumption that combustion goes to completion (i.e. CO2 and H2O), we can calculate the adiabatic flame temperature by hand either at stoichiometric conditions or lean of stoichiometry (excess air). This is because there are enough variables and molar equations to balance the left and right hand sides, Rich of stoichiometry there are not enough variables because combustion cannot go to completion with at least CO and H2 needed for the molar balance (these are the most common incomplete products of combustion), However, if we include the Water Gas Shift reaction, and use the equilibrium constant for this reaction, we will have enough variables to complete the calculation. Different fuels with different levels of energy and molar constituents will have different adiabatic flame temperatures.
We can see by the following figure why nitromethane (CH3NO2) is often used as a power boost for cars. Since it contains two moles of oxygen in its molecular makeup, it can burn much hotter because it provides its own oxidant along with fuel. This in turn allows it to build-up more pressure during a constant volume process. The higher the pressure, the more force upon the piston creating more work and more power in the engine. It is interesting to note that it stays relatively hot rich of stoichiometry because it contains its own oxidant. However, continual running of an engine on nitromethane will eventually melt the piston and/or cylinder because of this higher temperature.
In real world applications, complete combustion does not typically occur. Chemistry dictates that dissociation and kinetics will change the relative constituents of the products. There are a number of programs available that can calculate the adiabatic flame temperature taking into account dissociation through equilibrium constants (Stanjan, NASA CEA, AFTP). The following figure illustrates that the effects of dissociation tend to lower the adiabatic flame temperature. This result can be explained through Le Chatelier's principle. See also |
|||||||||||||||||||||||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Adiabatic_flame_temperature". A list of authors is available in Wikipedia. |





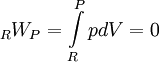
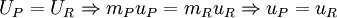 .
.
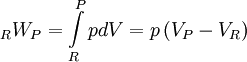
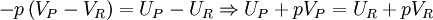
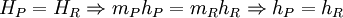 .
.