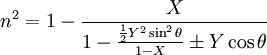To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Appleton-Hartree equationThe Appleton-Hartree equation, sometimes also referred to as the Appleton-Lassen equation is a mathematical expression that describes the refractive index for electromagnetic wave propagation in a cold magnetized plasma. The Appleton-Hartree equation was developed independently by several different scientists, including Edward Victor Appleton, Douglas Hartree and K. Lassen. Product highlight
EquationFull EquationThe equation is typically given as follows [1]: Definition of Termsn = complex refractive index i =
ν = electron collision frequency ω = 2πf f = wave frequency
ε0 = permittivity of free space μ0 = permeability of free space B0 = ambient magnetic field strength e = electron charge m = electron mass θ = angle between the ambient magnetic field vector and the wave vector Modes of PropagationThe presence of the Reduced FormsPropagation in a Collisionless PlasmaIf the wave frequency of interest ω is much smaller than the electron collision frequency ν, the plasma can be said to be "collisionless." That is, given the condition
we have
so we can neglect the Z terms in the equation. The Appleton-Hartree equation for a cold, collisionless plasma is therefore, Quasi-Longitudinal Propagation in a Collisionless PlasmaIf we further assume that the wave propagation is primarily in the direction of the magnetic field, i.e., References |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Appleton-Hartree_equation". A list of authors is available in Wikipedia. |





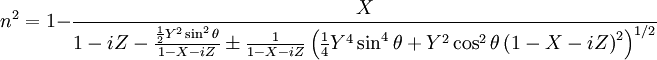
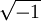
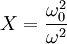
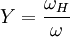
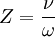
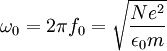 = electron
= electron 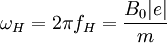 = electron gyro frequency
= electron gyro frequency
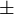 sign in the Appleton-Hartree equation gives two separate solutions for the refractive index
sign in the Appleton-Hartree equation gives two separate solutions for the refractive index 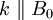 , the '+' sign represents the "ordinary mode," and the '-' sign represents the "extraordinary mode." For propagation perpendicular to the magnetic field, i.e.,
, the '+' sign represents the "ordinary mode," and the '-' sign represents the "extraordinary mode." For propagation perpendicular to the magnetic field, i.e., 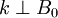 , the '+' sign represents a left-hand circularly polarized mode, and the '-' sign represents a right-hand circularly polarized mode. See the article on
, the '+' sign represents a left-hand circularly polarized mode, and the '-' sign represents a right-hand circularly polarized mode. See the article on 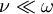 ,
,
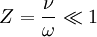 ,
,
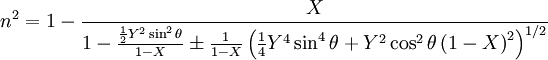
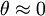 , we can neglect the
, we can neglect the