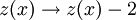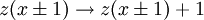Bak-Tang-Wiesenfeld sandpile

Additional recommended knowledge

What is the Sensitivity of my Balance?

How to quickly check pipettes?

Daily Sensitivity Test

In physics, the Bak-Tang-Wiesenfeld sandpile model is the first discovered example of a dynamical system displaying self-organized criticality and is named after Per Bak, Chao Tang and Kurt Wiesenfeld.

The model is a cellular automaton. At each site on the lattice there is a value that corresponds to the slope of the pile. This slope builds up as grains of sand are randomly placed onto the pile, until the slope exceeds a specific threshold value at which time that site collapses transferring sand into the adjacent sites, increasing their slope. This random placement of sand at a particular site may have no effect and it may cause a cascading reaction that will affect every site on the lattice. These "avalanches" are an example of the Eden growth model.

The iteration rules for the 2D model are as follows:

Starting with a flat surface z(x,y) = 0 for all x and y:
Add a grain of sand:

And avalanche if z(x,y) > z_c:

This system is interesting in that it is attracted to its critical state, at which point the correlation length of the system and the correlation time of the system go to infinity, without any fine tuning of a system parameter. This contrasts with earlier examples of critical phenomena, such as the phase transitions between solid and liquid, or liquid and gas, where the critical point can only be reached by precise tuning (usually of temperature). Hence, in the sandpile model we can say that the criticality is self-organized.

Once the sandpile model reaches its critical state there is no correlation between the system's response to a perturbation and the details of a perturbation. Generally this means that dropping another grain of sand onto the pile may cause nothing to happen, or it may cause the entire pile to collapse in a massive slide. The model also displays 1/f noise, a feature common to many complex systems in nature.

This model only displays critical behaviour in 2 or more dimensions. The sandpile model can be expressed in 1D, however instead of evolving to its critical state the 1D sandpile model instead reaches a minimally stable state where every lattice site goes toward the critical slope.

The iteration rules for the 1D model is:

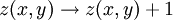
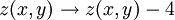
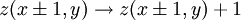
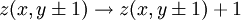
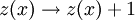Adding a grain of sand at x: And an avalanche at x if z > z_c:

References

• Bak, P. (1996). How Nature Works: The Science of Self-Organized Criticality. New York: Copernicus. ISBN 0-387-94791-4. 

• Bak, P., Tang, C. and Wiesenfeld, K. (1987). "Self-organized criticality: an explanation of 1 / f noise". Physical Review Letters 59: 381–384. doi:10.1103/PhysRevLett.59.381.

• Bak, P., Tang, C. and Wiesenfeld, K. (1988). "Self-organized criticality". Physical Review A 38: 364–374. doi:10.1103/PhysRevA.38.364.