To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Bekenstein boundIn physics, the Bekenstein bound is a conjectured limit on the entropy S or information that can be contained within a region of space containing a known energy. It implies that information must be material, requiring finite size and energy. In Computer Science, this implies that there is a maximum information processing rate and that Turing machines, with their (by definition) infinite memory tape, are physically impossible if they are to have a finite size and bounded energy. The bound was originally found by Jacob Bekenstein in the form
Product highlightwhere R is loosely defined as the radius of the region, and E is the energy of the contained matter as measured when the matter is moved to an infinite distance, i.e., accounting for binding force potential energies. Note that while gravity plays a significant role in its enforcement, the bound is independent of Newton's Constant G. Bekenstein derived the bound from heuristic arguments involving black holes. If a system exists that violates the bound, Bekenstein argued that it would be possible to violate the Second Law of Thermodynamics by lowering it into a black hole. However, no precise formulation of it is known, with the correct definitions of radius, energy and entropy all subject to debate. There is also considerable debate that any formulation of the bound exists. Although the derivation of the bound is only valid for weakly gravitating systems, it happens that the Bekenstein-Hawking Entropy of three-dimensional black holes exactly saturates the bound
where A is the two-dimensional area of the black hole's event horizon in units of the Planck area, The bound is closely associated with Black hole thermodynamics, the Holographic Principle and the Covariant Entropy Bound of quantum gravity, and can be derived from a conjectured strong form of the latter. However, while the bound played an important role alongside their development, these topics are generally on firmer theoretical footing than the Bekenstein Bound, with more precise formulations and more consistent theoretical support. See also
References
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Bekenstein_bound". A list of authors is available in Wikipedia. |


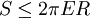 ,
,



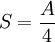 ,
,
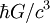 .
.


