To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Bidirectional reflectance distribution function
The bidirectional reflectance distribution function (BRDF;
Product highlight
ApplicationsThe BRDF is a fundamental radiometric concept, and accordingly is used in computer graphics for photorealistic rendering of synthetic scenes (see the Rendering equation), as well as in computer vision for many inverse problems such as object recognition. ModelsThe BRDF was first defined by Edward in mid sixties[1]. BRDFs can be measured directly from real objects using calibrated cameras and lightsources [2]; however, many phenomenological and analytic models have been proposed including the Lambertian reflectance model frequently assumed in computer graphics. Some noteworthy examples are the phenomenological Phong reflectance model, Ward's anisotropic reflectance model [3] , and the Torrance-Sparrow microfacet based reflection model [4]. AcquisitionTraditionally, BRDF measurements were taken for a specific lighting and viewing direction at a time using gonioreflectometers. Unfortunately, using such a device to densely measure the BRDF is very time consuming. One of the first improvements on these techniques used a half-silvered mirror and a digital camera to take many BRDF samples of a planar target at once [5]. Since this work, many researchers have developed other devices for efficiently acquiring BRDFs from real world samples, and it remains an active area of research. See also
Further Reading
References
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Bidirectional_reflectance_distribution_function". A list of authors is available in Wikipedia. |


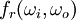 ) is a 4-dimensional function that defines how light is reflected at an opaque surface. The function takes an incoming light direction,
) is a 4-dimensional function that defines how light is reflected at an opaque surface. The function takes an incoming light direction, 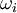 , and outgoing direction,
, and outgoing direction, 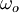 , both defined with respect to the surface normal
, both defined with respect to the surface normal 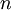 , and returns the ratio of reflected
, and returns the ratio of reflected 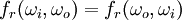 , and energy conservation. The BRDF has units sr-1, with
, and energy conservation. The BRDF has units sr-1, with 




