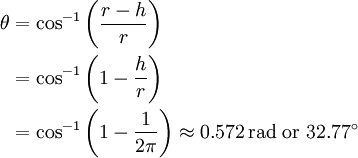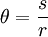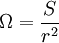To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Steradian
The steradian (symbol: sr) is the SI unit of solid angle. It is used to describe two-dimensional angular spans in three-dimensional space, analogous to the way in which the radian describes angles in a plane. The name is derived from the Greek stereos for "solid" and the Latin radius for "ray, beam". The steradian is dimensionless because 1 sr = m2·m-2 = 1. It is useful, however, to distinguish between dimensionless quantities of different nature, so in practice the symbol "sr" is used where appropriate, rather than the derived unit "1" or no unit at all. As an example, radiant intensity can be measured in watts per steradian (W·sr-1). Product highlight
DefinitionA single unit of steradian is defined as the solid angle subtended at the center of a sphere of radius r by a portion of the surface of the sphere having an area r2.
If this area This angle corresponds to an apex angle of 2θ ≈ 1.144 rad or 65.54°. Because the surface area of this sphere is 4πr2, then the definition implies that a sphere measures 4π steradians. By the same argument, the maximum solid angle that can be subtended at any point is 4π sr. A steradian can also be called a squared radian. A steradian is also equal to the spherical area of a polygon having an angle excess of 1 radian, to 1/4π of a complete sphere, or to (180/π)² or 3282.80635 square degrees. The steradian was formerly an SI supplementary unit, but this category was abolished from the SI in 1995 and the steradian is now considered an SI derived unit. Analogue to radiansIn two dimensions, the angle in radians is related to the arc length it cuts out:
Now in three dimensions, the solid angle in steradians is related to the area it cuts out:
SI multiples
See also
|
|||||||||||||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Steradian". A list of authors is available in Wikipedia. |





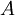 is equal to
is equal to 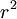 and it corresponds to the area of a spherical cap (
and it corresponds to the area of a spherical cap (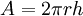 ) then the relationship
) then the relationship 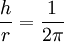 holds. Then the solid angle of the simple cone subtending an angle θ is equal to:
holds. Then the solid angle of the simple cone subtending an angle θ is equal to: