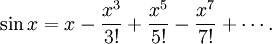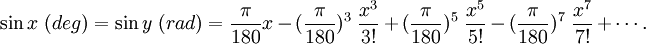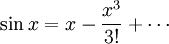To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Radian
The radian, in mathematics, is a unit of plane angle, equal to 180/π degrees, or about 57.2958 degrees. It is represented by the symbol "rad" or, more rarely, by the superscript c (for "circular measure"). For example, an angle of 1.2 radians would be written as "1.2 rad" or "1.2c" (the second symbol can be mistaken for a degree: "1.2°"). However, the radian is the standard unit of angular measurement for mathematicians, and in mathematical writing the symbol "rad" is almost always omitted. In the absence of any symbol radians are assumed, and when degrees are meant the symbol ° is used. The radian was formerly an SI supplementary unit, but this category was abolished in 1995 and the radian is now considered an SI derived unit. The SI unit of solid angle measurement is the steradian. Product highlight
Definition
One radian is the angle subtended at the center of a circle by an arc of circumference that is equal in length to the radius of the circle. More generally, the magnitude in radians of any angle subtended by two radii is equal to the ratio of the length of the enclosed arc to the radius of the circle; that is, θ = s /r, where θ is the subtended angle in radians, s is arc length, and r is radius. Conversely, the length of the enclosed arc is equal to the radius multiplied by the magnitude of the angle in radians; that is, s = rθ. It follows that the magnitude in radians of one complete revolution (360 degrees) is the length of the entire circumference divided by the radius, or 2πr /r, or 2π. Thus 2π radians is equal to 360 degrees, meaning that one radian is equal to 180/π degrees. HistoryThe concept of radian measure, as opposed to the degree of an angle, should probably be credited to Roger Cotes in 1714.[1] He had the radian in everything but name, and he recognized its naturalness as a unit of angular measure. The term radian first appeared in print on June 5, 1873, in examination questions set by James Thomson (brother of Lord Kelvin) at Queen's College, Belfast. He used the term as early as 1871, while in 1869, Thomas Muir, then of the University of St Andrews, vacillated between rad, radial and radian. In 1874, Muir adopted radian after a consultation with James Thomson.[2][3][4] ConversionsConversion between radians and degreesAs stated above, one radian is equal to 180/π degrees. Thus, to convert from radians to degrees, multiply by 180/π. For example, Conversely, to convert from degrees to radians, multiply by π/180. For example, You can also convert radians to revolutions by dividing number of radians by 2π. The table shows the conversion of some common angles.
Conversion between radians and grads2π radians are equal to one complete revolution, which is 400g. So, to convert from radians to grads multiply by 200/π, and to convert from grads to radians multiply by π/200. For example, Reasons that radians are preferred in mathematicsIn calculus and most other branches of mathematics beyond practical geometry, angles are universally measured in radians. One important reason is that results in analysis involving trigonometric functions are simple and "natural" when the function's argument is expressed in radians. For example, the use of radians leads to the simple limit formula
which is the basis of many other elegant identities in mathematics, including
The trigonometric functions also have simpler series expansions when radians are used; for example, the following Taylor series for sin x : If x were expressed in degrees then the series would contain messy factors involving powers of π/180: if x is the number of degrees, the number of radians is y = πx /180, so Dimensional analysisAlthough the radian is a unit of measure, it is a dimensionless quantity. This can be seen from the definition given earlier: the angle subtended at the centre of a circle, measured in radians, is the ratio of the length of the enclosed arc to the length of the circle's radius. Since the units of measurement cancel, this ratio is dimensionless. Another way to see the dimensionlessness of the radian is in the series representations of the trigonometric functions, such as the Taylor series for sin x mentioned earlier: If x had units, then the sum would be meaningless: the linear term x cannot be added to (or have subtracted) the cubic term x3 / 3!. Therefore, x must be dimensionless. Use in physicsThe radian is widely used in physics when angular measurements are required. For example, angular velocity is typically measured in radians per second (rad/s). One revolution per second is equal to 2π radians per second. Similarly, angular acceleration is often measured in radians per second per second (rad/s2). The reasons are the same as in mathematics. Multiples of radian unitsMetric prefixes have limited use with radians, and none in mathematics. The milliradian (0.001 rad, or 1 mrad) is used in gunnery and targeting, because it corresponds to an error of 1 m at a range of 1000 m (at such small angles, the curvature is negligible). The divergence of laser beams is also usually measured in milliradians. Smaller units like microradians (μrads) and nanoradians (nrads) are used in astronomy, and can also be used to measure the beam quality of lasers with ultra-low divergence. Similarly, the prefixes smaller than milli- are potentially useful in measuring extremely small angles. However, the larger prefixes have no apparent utility, mainly because to exceed 2π radians is to begin the same circle (or revolutionary cycle) again. See also
References |
|||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Radian". A list of authors is available in Wikipedia. |





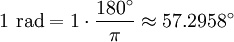
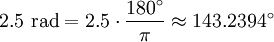
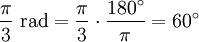
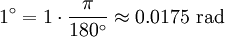
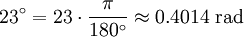
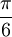
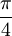
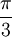
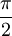
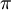
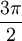
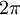
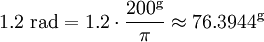
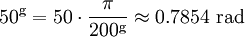
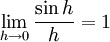 ,
,
 .
.