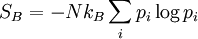Boltzmann entropy

In thermodynamics, specifically in statistical mechanics, the Boltzmann entropy is an approximation to the normal Gibbs entropy.

Additional recommended knowledge

Don't let static charges disrupt your weighing accuracy

Guide to balance cleaning: 8 simple steps

Weighing the right way

The Boltzmann entropy is obtained if one assumes one can treat all the component particles of a thermodynamic system as statistically independent. The probability distribution of the system as a whole then factorises into the product of N separate identical terms, one term for each particle; and the Gibbs entropy simplifies to the Boltzmann entropy

where the summation is taken over each possible state in the 6-dimensional phase space of a single particle (rather than the 6N-dimensional phase space of the system as a whole).

This reflects the original statistical entropy function introduced by Ludwig Boltzmann in 1872. For the special case of an ideal gas it exactly corresponds to the proper thermodynamic entropy.

However, for anything but the most dilute of real gases, it leads to increasingly wrong predictions of entropies and physical behaviours, by ignoring the interactions and correlations between different molecules Instead one must follow Gibbs, and consider the ensemble of states of the system as a whole, rather than single particle states.

See also

• Entropy (thermodynamics)
• Boltzmann's entropy formula
• Gibbs entropy

References

• Jaynes, E. T. (1965). Gibbs vs Boltzmann entropies. American Journal of Physics, 33, 391-8.