To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Bounded deformationIn mathematics, a function of bounded deformation is a function whose distributional derivatives are not quite well-behaved-enough to qualify as functions of bounded variation, although the symmetric part of the derivative matrix does meet that condition. Thought of as deformations of elasto-plastic bodies, functions of bounded deformation play a major role in the mathematical study of materials, e.g. the Francfort-Marigo model of brittle crack evolution. Product highlightMore precisely, given an open subset Ω of Rn, a function u : Ω → Rn is said to be of bounded deformation if the symmetrized gradient ε(u) of u, is a bounded, symmetric n × n matrix-valued Radon measure. The collection of all functions of bounded deformation is denoted BD(Ω; Rn), or simply BD. BD is a strictly larger space than the space BV of functions of bounded variation. One can show that if u is of bounded deformation then the measure ε(u) can be decomposed into three parts: one absolutely continuous with respect to Lebesgue measure, denoted e(u) dx; a jump part, supported on a rectifiable (n − 1)-dimensional set Ju of points where u has two different approximate limits u+ and u−, together with a normal vector νu; and a "Cantor part", which vanishes on Borel sets of finite Hn−1-measure (where Hk denotes k-dimensional Hausdorff measure). A function u is said to be of special bounded deformation if the Cantor part of ε(u) vanishes, so that the measure can be written as where H n−1 | Ju denotes H n−1 on the jump set Ju and The collection of all functions of bounded deformation is denoted SBD(Ω; Rn), or simply SBD. References
Categories: Materials science | Solid mechanics |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Bounded_deformation". A list of authors is available in Wikipedia. |





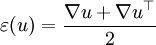
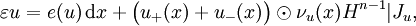
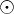 denotes the symmetrized dyadic product:
denotes the symmetrized dyadic product: