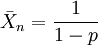To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Carothers equationIn step-growth polymerization, the Carothers equation (or Carothers' equation) gives the number-average degree of polymerization, Xn, for a given fractional monomer conversion, p. Product highlightThis equation was proposed by Wallace Carothers who invented nylon in 1935. Notes:
A high monomer conversion is required to achieve a high number-average degree of polymerization. For example, a monomer conversion, p, of 98% is required for Xn = 50, and p = 99% is required for Xn = 100.
Related equationsRelated to the Carothers equation are the following equations: where:
The last equation shows that the maximum value of the PDI is 2, which occurs at a monomer conversion of 100%. In practice the average length of the polymer chain is limited by such things as the purity of the reactants, the absence of any side reactions (i.e. high yield), and the viscosity of the medium. |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Carothers_equation". A list of authors is available in Wikipedia. |
- Jablonski_diagram
- Clavulanic_acid
- Artificial intelligence designs advanced materials - Scientists of the Max-Planck-Institut für Eisenforschung pioneer new machine learning model for corrosion-resistant alloy design
- Isotopes_of_americium
- Photocatalysis: Processes in charge separation recorded experimentally - The results provide clues to increase the efficiency of photocatalysts