To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
CatenoidA catenoid is a three-dimensional shape made by rotating a catenary curve around the x axis. Not counting the plane, it is the first minimal surface to be discovered. It was found by Leonhard Euler in 1744. Product highlightA physical model of a catenoid can be formed by dipping two circles into a soap solution and slowly drawing the circles apart.
One can bend a catenoid into the shape of a helicoid without stretching. In other words, one can make a continuous and isometric deformation of a catenoid to a helicoid such that every member of the deformation family is minimal. A parametrization of such a deformation is given by the system
for |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Catenoid". A list of authors is available in Wikipedia. |
- Solving stability problems of relevant graphene derivatives - An international team involving chemists, physicists and materials scientists implements protection/deprotection strategies for the on-surface synthesis of technologically prominent graphene nanostructures
- Daniel_Rutherford
- BASF démarre l'exploitation commerciale de l'usine Black Mass pour le recyclage des batteries à Schwarzheide, en Allemagne
- MorphoSys Reaches Milestone with Bayer
- DyStar Singapore Pte Ltd - Singapore, Cingapura





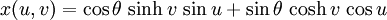
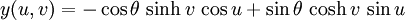
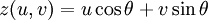
![(u,v) \in (-\pi, \pi] \times (-\infty, \infty)](images/math/d/1/1/d11b64d7f07089a4a1d3fded937de015.png) , with deformation parameter
, with deformation parameter 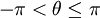 .
.


