To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Cebeci-Smith modelThe Cebeci-Smith model is a 0-equation eddy viscosity model used in computational fluid dynamics analysis of turbulent boundary layer flows. The model gives eddy viscosity, μt, as a function of the local boundary layer velocity profile. The model is suitable for high-speed flows with thin attached boundary-layers, typically present in aerospace applications. Like the Baldwin-Lomax model, this model is not suitable for cases with large separated regions and significant curvature/rotation effects. Unlike the Baldwin-Lomax model, this model requires the determination of of a boundary layer edge. Product highlightEquationsIn a two-layer model, the boundary layer is considered to comprise two layers: inner (close to the surface) and outer. The eddy viscosity is calculated separately for each layer and combined using: where ycrossover is the smallest distance from the surface where The inner-region eddy viscosity is given by: where with the von Karman constant κ usually being taken as 0.4, and with The eddy viscosity in the outer region is given by: where α = 0.0168, and FK is the Klebanoff intermittency function given by References
Categories: Turbulence models | Fluid dynamics |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Cebeci-Smith_model". A list of authors is available in Wikipedia. |





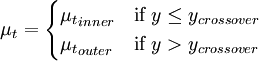
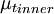 is equal to
is equal to 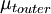 .
.
![{\mu_t}_{inner} = \rho l^2 l \left[\left( \frac{\partial U}{\partial y}\right)^2 + \left(\frac{\partial V}{\partial x}\right)^2 \right]^{1/2}](images/math/6/5/f/65fb0bf910ff1abb94f4f9f8ebeb33cb.png)
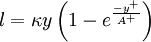
![A^+ = 26\left[1+y\frac{dP/dx}{\rho u_\tau^2}\right]^{-1/2}](images/math/2/8/a/28a902f9e8999378da20ff20b304aaf1.png)
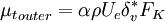
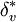 is the
is the 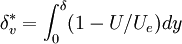
![F_{K} = \left[1 + 5.5 \left( \frac{y}{\delta} \right)^6 \right]^{-1}](images/math/d/e/6/de6ec5a827979b627e823c008ace6c69.png)


