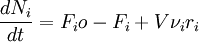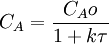Continuous stirred-tank reactor

The continuous stirred-tank reactor (CSTR), also known as vat- or backmix reactor, is a common ideal reactor type in chemical engineering. A CSTR often refers to a model is used to estimate the key unit operation variables when using a continuous agitated-tank reactor to reach a specified output. (See Chemical reactors.) The mathematical model works for all fluids: liquids, gases, and slurries.

Additional recommended knowledge

What is the Sensitivity of my Balance?

Guide to balance cleaning: 8 simple steps

Essential Laboratory Skills Guide

Assume:

• perfect mixing - This is a fair assumption because merely requires the region of variable composition at the inlet area is very small when compared to the entire reactor contents and the time required to mix tank contents is very small when compared to the residence time of the reactor. This assumption is required for the model due to the strong dependence of the reaction rate on the concentration of the reagent species.

Integral mass balance on number of moles N_i of species i in a reactor of volume V.

[accumulation] = [in] - [out] + [generation]

1. ^[1]

where F_io is the molar flow rate inlet of species i, F_i the molar flow rate outlet, and ν_i stoichiometric coefficient. The reaction rate, r, is generaly depentant on the reactant concentation and the rate constant (k). The rate constant can be figured by using the Arrhenius temperature dependence. Generally, as the temperature increases so does the rate at which the reaction occurs. Residence time, τ, is the average amount of time a discrete quantity of reagent spends inside the tank.

Assume:

• constant density (valid for most liquids; valid for gases only if there is no net change in the number of moles or drastic temperature change)
• isothermal conditions, or constant temperature (k is constant)
• steady state
• single, irreversible reaction (ν_A = -1)
• first-order reaction (r = kC_A)

A → products

N_A = C_A V (where C_A is the concentration of species A, V is the volume of the reactor, N_A is the number of moles of species A)

2. ^[1]

The values of the variables, outlet concentration and residence time, in Equation 2 are major design criteria.

To model systems that do not obey the assumptions of constant temperature and a single reaction, additional dependent variables must be considered. If the system is considered to be in unsteady-state, a differential equation or a system of coupled differential equations must be solved.

CSTR's are known to be one of the systems which exhibit complex behavior such as steady-state multiplicity, limit cycles and chaos.

See also

• Chemical reactors
• Chemical reactions
• Chemostat

References

1. ^ ^{a b} Schmidt, Lanny D. (1998). The Engineering of Chemical Reactions. New York: Oxford University Press. ISBN 0-19-510588-5.