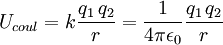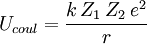To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Coulomb barrierThe Coulomb barrier, named after physicist Charles-Augustin de Coulomb (1736–1806), is the energy barrier due to electrostatic interaction that two nuclei need to overcome so they can get close enough to undergo nuclear fusion. This energy barrier is given by the electrostatic potential energy: Product highlightwhere
A positive value of U is due to a repulsive force, so interacting particles get at higher energy levels when they get closer. A negative potential energy indicates a bound state (due to an attractive force). Coulomb's barrier increases with the atomic numbers (i.e. the number of protons) of the colliding nuclei: where e is the elementary charge, 1.602 176 53×10−19 C, and Zi the corresponding atomic numbers. To overcome this barrier nuclei have to collide at high velocities, so their kinetic energies drive them close enough for the strong interaction to take place and bind them together. According to the kinetic theory of gases, the temperature of a gas is just a measure of the average velocity of the particles in that gas. For normal gases, the Maxwell-Boltzmann distribution gives the fraction of particles moving at a given velocity as a function of gas temperature, and thus the fraction of particles moving at velocities high enough to overcome the Coulomb's barrier can be derived. In practice, temperatures needed to overcome Coulomb's barrier turn out to be smaller than expected due to quantum-mechanical tunneling, as established by Gamow. The consideration of barrier-penetration through tunneling and the speed distribution gives rise to a limited range of conditions where the fusion can take place, known as the Gamow window. |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Coulomb_barrier". A list of authors is available in Wikipedia. |