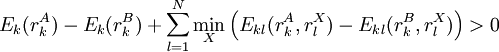To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Dead-end eliminationThe dead-end elimination algorithm (DEE) is a method for minimizing a function over a discrete set of independent variables. The basic idea is to identify "dead ends", i.e., "bad" combinations of variables that cannot possibly yield the global minimum and to refrain from searching such combinations further. Hence, dead-end elimination is a mirror image of dynamic programming and memoization, optimization techniques in which "good" combinations are identified and explored further. Although the method itself is general, it has been developed and applied mainly to the problems of predicting and designing the structures of proteins. The original description and proof of the dead-end elimination theorem can be found in . Product highlight
Basic requirementsAn effective DEE implementation requires four pieces of information:
Note that the criteria can easily be reversed to identify the maximum of a given function as well. Applications to protein structure predictionDead-end elimination has been used effectively to predict the structure of side chains on a given protein backbone structure by minimizing an energy function E. The dihedral angle search space of the side chains is restricted to a discrete set of rotamers for each amino acid position in the protein (which is, obviously, of fixed length). The original DEE description included criteria for the elimination of single rotamers and of rotamer pairs, although this can be expanded.
Singles elimination criterionIf a particular rotamer
Pairs elimination criterionThe pairs criterion is more difficult to describe and to implement, but it adds significant eliminating power. For brevity, we define the shorthand variable A given pair of rotamers A and B at positions k and l, respectively, cannot both be in the final solution (although one or the other may be) if there is another pair C and D that always gives a better energy. Expressed mathematically, where Energy matricesFor large N, the matrices of precomputed energies can become costly to store. Let N be the number of amino acid positions, as above, and let p be the number of rotamers at each position (this is usually, but not necessarily, constant over all positions). Each self-energy matrix for a given position requires p entries, so the total number of self-energies to store is Np. Each pair energy matrix between two positions rk and rl, for p discrete rotamers at each position, requires a Implementation and efficiencyThe above two criteria are normally applied iteratively until convergence, defined as the point at which no more rotamers or pairs can be eliminated. Since this is normally a reduction in the sample space by many orders of magnitude, simple enumeration will suffice to determine the minimum within this pared-down set. Given this model, it is clear that the DEE algorithm is guaranteed to find the optimal solution; that is, it is a global optimization process. The single-rotamer search scales quadratically in time with total number of rotamers. The pair search scales cubically and is the slowest part of the algorithm (aside from energy calculations). This is a dramatic improvement over the brute-force enumeration which scales as O(pN). A large-scale benchmark of DEE compared with alternative methods of protein structure prediction and design finds that DEE reliably converges to the optimal solution for protein lengths for which it runs in a reasonable amount of time. It significantly outperforms the alternatives under consideration, which involved techniques derived from mean field theory, genetic algorithms, and the Monte Carlo method. However, the other algorithms are appreciably faster than DEE and thus can be applied to larger and more complex problems; their relative accuracy can be extrapolated from a comparison to the DEE solution within the scope of problems accessible to DEE. Protein designThe preceding discussion implicitly assumed that the rotamers rk are all different orientations of the same amino acid side chain. That is, the sequence of the protein was assumed to be fixed. It is also possible to allow multiple side chains to "compete" over a position k by including both types of side chains in the set of rotamers for that position. This allows a novel sequence to be designed onto a given protein backbone. A short zinc finger protein fold has been redesigned this way. However, this greatly increases the number of rotamers per position and still requires a fixed protein length. GeneralizationsMore powerful and more general criteria have been introduced that improve both the efficiency and the eliminating power of the method for both prediction and design applications. One example is a refinement of the singles elimination criterion known as the Goldstein criterion, which arises from fairly straightforward algebraic manipulation before applying the minimization: Thus rotamer An extended discussion of elaborate DEE criteria and a benchmark of their relative performance can be found in . References
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Dead-end_elimination". A list of authors is available in Wikipedia. |





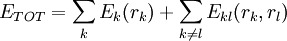
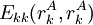 (that is, the pair energy between a rotamer and itself) is taken to be zero, and thus does not affect the summations. This notation simplifies the description of the pairs criterion below.
(that is, the pair energy between a rotamer and itself) is taken to be zero, and thus does not affect the summations. This notation simplifies the description of the pairs criterion below.
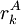 of sidechain
of sidechain 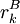 of the same sidechain, then rotamer A can be eliminated from further consideration, which reduces the search space. Mathematically, this condition is expressed by the inequality
of the same sidechain, then rotamer A can be eliminated from further consideration, which reduces the search space. Mathematically, this condition is expressed by the inequality
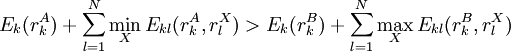
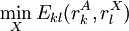 is the minimum (best) energy possible between rotamer
is the minimum (best) energy possible between rotamer 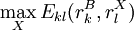 is the maximum (worst) energy possible between rotamer
is the maximum (worst) energy possible between rotamer 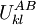 that is the intrinsic energy of a pair of rotamers
that is the intrinsic energy of a pair of rotamers 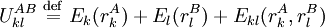
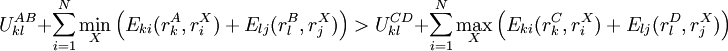
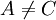 ,
, 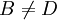 and
and 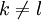 .
.
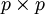 matrix. This makes the total number of entries in an unreduced pair matrix
matrix. This makes the total number of entries in an unreduced pair matrix