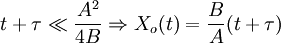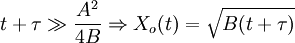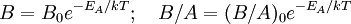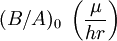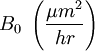To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Deal-Grove modelThe Deal-Grove model mathematically describes the growth of an oxide layer on the surface of a material. In particular, it is used to analyze thermal oxidation of silicon in semiconductor device fabrication. The model was first published in 1965 by Bruce Deal and Andrew Grove, of Fairchild Semiconductor. Product highlight
Physical assumptionsThe model assumes that oxidation reaction occurs at the interface between the oxide and the substrate, rather than between the oxide and the ambient gas. Thus, it considers three phenomena that the oxidizing species undergoes, in this order:
The model assumes that each of these stages proceeds at a rate proportional to the oxidant's concentration. In the first case, this means Henry's law; in the second, Fick's law of diffusion; in the third, a first-order reaction with respect to the oxidant. It also assumes steady state conditions, i.e. that transient effects do not appear. ResultsGiven these assumptions, the flux of oxidant through each of the three phases can be expressed in terms of concentrations, material properties, and temperature. By setting the three fluxes equal to each other, they may each be found. In turn, the growth rate may be found readily from the oxidant reaction flux. In practice, the ambient gas (stage 1) does not limit the reaction rate, so this part of the equation is often dropped. This simplification yields a simple quadratic equation for the oxide thickness. For oxide growing on an initially bare substrate, the thickness Xo at time t is given by the following equation: where the constants A and B encapsulate the properties of the reaction and the oxide layer, respectively. If a wafer that already contains oxide is placed in an oxidizing ambient, this equation must be modified by adding a corrective term τ, the time that would have been required to grow the pre-existing oxide under current conditions. This term may be found using the equation for t above. Solving the quadratic equation for Xo yields: The discriminant of the above equation reveals two main modes of operation: Because they appear in these equations, the quantities B and B/A are often called the quadratic and linear reaction rate constants. They depend exponentially on temperature, like this: where EA is the activation energy. EA differs from one equation to the other. The following table lists the values of the four parameters for single-crystal silicon under conditions typically used in industry (low doping, atmospheric pressure). The linear rate constant depends on the orientation of the crystal (usually indicated by the Miller indices of the crystal plane facing the surface). The table gives values for <100> and <111> silicon.
Validity for siliconThe Deal-Grove model works very well for single-crystal silicon under most conditions. However, experimental data shows that very thin oxides (less than about 25 nanometres) grow much more quickly in O2 than the model predicts. This phenomenon is not well understood theoretically, but it can be modeled. If the oxide grown in a particular oxidation step will significantly exceed 25 nm, a simple adjustment accounts for the aberrant growth rate. The model yields accurate results for thick oxides if, instead of assuming zero initial thickness (or any initial thickness less than 25 nm), we assume that 25 nm of oxide exists before oxidation begins. However, for oxides near to or thinner than this threshold, more sophisticated models must be used. Deal-Grove also fails for polycrystalline silicon ("poly-silicon"). First, the random orientation of the crystal grains makes it difficult to choose a value for the linear rate constant. Second, oxidant molecules diffuse rapidly along grain boundaries, so that poly-silicon oxidizes more rapidly than single-crystal silicon. Dopant atoms strain the silicon lattice, and make it easier for silicon atoms to bond with incoming oxygen. This effect may be neglected in many cases, but heavily-doped silicon oxidizes significantly faster. The pressure of the ambient gas also affects oxidation rate. References
|
|||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Deal-Grove_model". A list of authors is available in Wikipedia. |





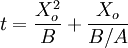
![X_o(t) = A/2 \cdot \left[ \sqrt{1+\frac{4B}{A^2}(t+\tau)} - 1 \right]](images/math/3/1/0/31047436a8a731420a4520a74f0a76fb.png)