My watch list

Debye relaxation

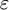Debye relaxation is the dielectric relaxation response of an ideal, noninteracting population of dipoles to an alternating external electric field. It is usually expressed in the complex permittivity $\varepsilon$ of a medium as a function of the field's frequency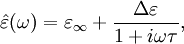 $ω$ :

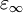$\hat{\varepsilon}(\omega) = \varepsilon_{\infty} + \frac{\Delta\varepsilon}{1+i\omega\tau},$

Additional recommended knowledge

Weighing the right way

Better weighing performance in 6 easy steps

Essential Laboratory Skills Guide

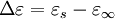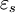where $\varepsilon_{\infty}$ is the permittivity at the high frequency limit, $\Delta\varepsilon = \varepsilon_{s}-\varepsilon_{\infty}$ where $\varepsilon_{s}$ is the static, low frequency permittivity, and $τ$ is the characteristic relaxation time of the medium.