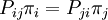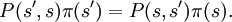Detailed balance

In mathematics and statistical mechanics, a Markov process is said to show detailed balance if the transition rates between each pair of states i and j in the state space obey

Additional recommended knowledge

Safe Weighing Range Ensures Accurate Results

Essential Laboratory Skills Guide

Daily Sensitivity Test

where P is the Markov transition matrix (transition probability), ie P_ij = P( X_t =j | X_t−1 = i ); and π_i and π_j are the equilibrium probabilities of being in states i and j, respectively.

The definition carries over straightforwardly to continuous variables, where π becomes a probability density, and P a transition kernel:

A Markov process that satisfies the detailed balance equations is said to be a reversible Markov process or reversible Markov chain with respect to π.

Note that the detailed balance condition is stronger than that required merely for a stationary distribution. It applies separately pairwise to each pair of states, so a steady-state probability current A -> B -> C -> A does not suffice.

Detailed balance is a weaker condition than requiring the transition matrix be symmetric, P_ij = P_ji. That would imply that the uniform distribution over the states would automatically be an equilibrium distribution. However, for continuous systems it may be possible to continuously transform the co-ordinates until a uniform metric is the equilibrium distribution, with a transition kernel which then is symmetric. In the discrete case it may be possible to achieve something similar, by breaking the Markov states into a degeneracy of sub-states.

Such an invariance is a supporting justification for the principle of equal a-priori probability in statistical mechanics.

See also

• Gibbs sampling
• Master equation
• Atomic spectral line (deduction of the Einstein coefficients)
• Random walks on graphs
• DMP