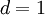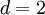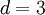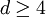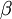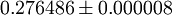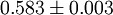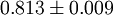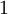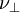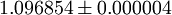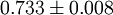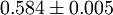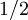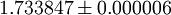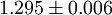To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Directed percolation
In statistical physics Directed Percolation (DP) refers to a class of models that mimic filtering of fluids through porous materials along a given direction. Varying the microscopic connectivity of the pores, these models display a phase transition from a macroscopically permeable (percolating) to an impermeable (non-percolating) state. Directed Percolation is also used as a simple model for epidemic spreading with a transition between survival and extinction of the disease depending on the infection rate. More generally, the term Directed Percolation stands for a universality class of continuous phase transitions which are characterized by the same type of collective behavior on large scales. Directed Percolation is probably the simplest universality class of transitions out of thermal equilibrium. Product highlight
Lattice models of Directed Percolation
One of the simplest realizations of DP is bond directed percolation. This model is a directed variant of ordinary (isotropic) percolation and can be introduced as follows. The figure shows a tilted square lattice with bonds connecting neighboring sites. The bonds are permeable (open) with probability The difference between ordinary and directed percolation is illustrated below. In isotropic percolation a spreading agent (e.g. water) introduced at a particular site marked by a green circle percolates along open bonds, generating a certain cluster of wet sites. Contrarily, in directed percolation the spreading agent can pass open bonds only along a preferred direction in space, as indicated by the arrow. The resulting cluster is directed in space.
Directed Percolation as a dynamical processInterpreting the preferred direction as a temporal degree of freedom, directed percolation can be regarded as a stochastic process that evolves in time. In the case of bond DP the time parameter t is discrete and all sites are updated in parallel. Activating a certain site (called initial seed) at time t = 0 the resulting cluster can be constructed row by row. As shown in the figure, the corresponding number of active sites N(t) varies as time evolves.
Universal scaling behaviorThe DP universality class is characterized by a certain set of critical exponents. These exponents depend on the spatial dimension
Other examplesIn two dimensions, the percolation of water through a thin tissue (such as toilet paper) has the same mathematical underpinnings as the flow of electricity through two-dimensional random networks of resistors. In chemistry, chromatography can be understood with similar models. The propagation of a tear or rip in a sheet of paper, in a sheet of metal, or even the formation of a crack in ceramic bears broad mathematical resemblance to the flow of electricity through a random network of electrical fuses. Above a certain critical point, the electrical flow will cause a fuse to pop, possibly leading to a cascade of failures, resembling the propagation of a crack or tear. The study of percolation helps indicate how the flow of electricity will redistribute itself in the fuse network, thus modeling which fuses are most likely to pop next, and how fast they will pop, and what direction the crack may curve in. Examples can be found not only in physical phenomena, but also in biological and ecological ones (evolution), and also in economic and social ones (see diffusion of innovation). Percolation can be considered to be a branch of the study of dynamical systems or statistical mechanics. In particular, percolation networks exhibit a phase change around a critical threshold. Open problemsSo far no experiment is known that reproduces the critical behavior of DP quantitatively, in particular the values of the critical exponents. Designing and performing such an experiment remains a challenging open problem. SourcesLiterature
References
See also
|
|||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Directed_percolation". A list of authors is available in Wikipedia. |





 and impermeable (closed) otherwise. The sites and bonds may be interpreted as holes and randomly distributed channels of a porous medium.
and impermeable (closed) otherwise. The sites and bonds may be interpreted as holes and randomly distributed channels of a porous medium.
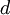 . Above the so-called upper critical dimension
. Above the so-called upper critical dimension 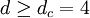 they are given by their mean-field values while in
they are given by their mean-field values while in
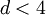 dimensions they have been estimated numerically. Current estimates are summarized in the following table:
dimensions they have been estimated numerically. Current estimates are summarized in the following table: