My watch list

Dyson series

In scattering theory, the Dyson series is a perturbative series, and each term is represented by Feynman diagrams. This series diverges asymptotically, but in quantum electrodynamics at the second order the difference from experimental data is in the order of $10 - 10$ . We get this result because the coupling constant of QED (also known as the fine structure constant) is much less than 1. Notice that in this article ħ = 1.

Additional recommended knowledge

How to quickly check pipettes?

Daily Visual Balance Check

The Dyson operator

We suppose we have a Hamiltonian H which we split into a "free" part H₀ and an "interacting" part V i.e. H=H₀+V. We will work in the interaction picture here.

In the interaction picture, the evolution operator U defined by the equation:

Ψ(t) = U (t, t 0)Ψ(t 0)

is called Dyson operator.

We have

$U(t,t)=I,\ U(t,t_0)=U(t,t_1)U(t_1,t_0),\ U^{-1}(t,t_0)=U(t_0,t)$

and then (Tomonaga-Schwinger equation)

$i{d \over dt} U(t,t_0)\Psi(t_0) = V(t) U(t,t_0)\Psi(t_0).$

Thus:

$U(t,t_0)=1 - i \int_{t_0}^t{dt_1\ V(t_1)U(t_1,t_0)}.$

Derivation of the Dyson series

This leads to the following Neumann series:

$U(t,t_0)=1 - i \int_{t_0}^{t}{dt_1V(t_1)}+(-i)^2\int_{t_0}^t{dt_1\int_{t_0}^{t_1}{dt_2V(t_1)V(t_2)}}+...+(-i)^n\int_{t_0}^t{dt_1\int_{t_0}^{t_1}{dt_2...\int_{t_0}^{t_{n-1}}{dt_nV(t_1)V(t_2)...V(t_n)}}}$

If we assume that $t > t 1 > t 2 > ... > t n$ we can say that the fields are time ordered, and so it is useful to introduce an operator called time-ordering operator. Defining:

$U_n(t,t_0)=(-i)^n\int_{t_0}^t{dt_1\int_{t_0}^{t_1}{dt_2...\int_{t_0}^{t_{n-1}}{dt_n\mathcal TV(t_1)V(t_2)...V(t_n)}}}$

We can now try to make this integration simpler. in fact, in the following example:

$S_n=\int_{t_0}^t{dt_1\int_{t_0}^{t_1}{dt_2...\int_{t_0}^{t_{n-1}}{dt_nK(t_1, t_2,...,t_n)}}}$

If K is symmetric in its arguments, we can define (look at integration limits):

$K_n=\int_{t_0}^t{dt_1\int_{t_0}^{t}{dt_2...\int_{t_0}^t{dt_nK(t_1, t_2,...,t_n)}}}$

And so it is true that:

$S_n=\frac{1}{n!}K_n$

Returning to our previous integral, it holds the identity:

$U_n=\frac{(-i)^n}{n!}\int_{t_0}^t{dt_1\int_{t_0}^t{dt_2...\int_{t_0}^t{dt_n\mathcal TV(t_1)V(t_2)...V(t_n)}}}$

Summing up all the terms we obtain the Dyson series:

$U(t,t_0)=\sum_{n=0}^\infty U_n(t,t_0)=\mathcal Te^{-i\int_{t_0}^t{d\tau V(\tau)}}$

The Dyson series for wavefunctions

Then, going back to the wavefunction for t>t₀,

$|\psi(t)\rangle=\sum_{n=0}^\infty {(-i)^n\over n!}\left(\prod_{k=1}^n \int_{t_0}^t dt_k\right) \mathcal{T}\left\{\prod_{k=1}^n e^{iH_0 t_k}Ve^{-iH_0 t_k}\right \}|\psi(t_0)\rangle$ .

Returning to the Schrödinger picture, for t_f > t_i,

$\langle\psi_f;t_f|\psi_i;t_i\rangle=\sum_{n=0}^\infty (-i)^n\begin{matrix}\underbrace{\int dt_1 \cdots dt_n}\\t_f\ge t_1\ge \dots\ge t_n\ge t_i\end{matrix}\langle\psi_f;t_f|e^{-iH_0(t_f-t_1)}Ve^{-iH_0(t_1-t_2)}\cdots Ve^{-iH_0(t_n-t_i)}|\psi_i;t_i\rangle$ .

References

Charles J. Joachain, Quantum collision theory, North-Holland Publishing, 1975, ISBN 0-444-86773-2 (Elsevier)

Category: Scattering theory

This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Dyson_series". A list of authors is available in Wikipedia.

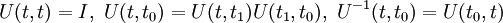
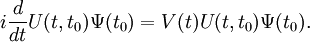
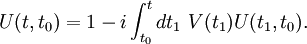
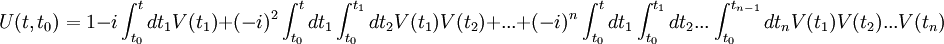
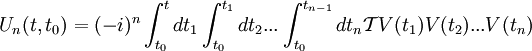
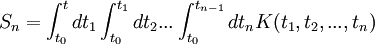
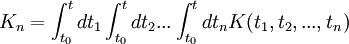
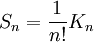
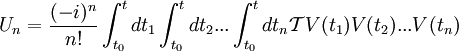
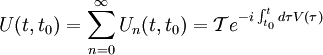
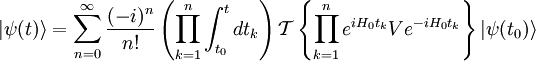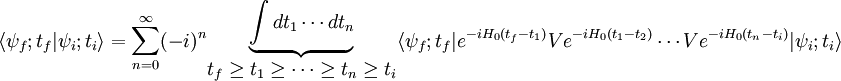Dyson series

Additional recommended knowledge

How to quickly check pipettes?

Daily Visual Balance Check

Weighing the right way

Contents

The Dyson operator

Derivation of the Dyson series

The Dyson series for wavefunctions

References

About chemeurope.com

About LUMITOS

Advertise with LUMITOS