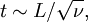Ekman layer

In standard boundary-layer theory, the effects of viscous diffusion are usually balanced by convective inertia. When a fluid rotates, however, the dominant balance may instead be struck between diffusion effects and the Coriolis force. Under these circumstances we are dealing with an Ekman layer.

Additional recommended knowledge

What is the Sensitivity of my Balance?

How to quickly check pipettes?

Correct Test Weight Handling Guide: 12 Practical Tips

In addition to enforcing the zero velocity condition at the wall, these Ekman layers can also control long-range properties of the flow. A classical illustration is given by the everyday experience of how a cup of tea returns to rest after stirring. We might model this from the decay of the rigid body motion through dissipative effects, which reach out from the stationary sides of the cup over a diffusion timescale

where L here is the cup radius. However, the spin-down times in real cups are much shorter than this, and to calculate the correct rate of decay we must consider the Ekman layer which has formed at the bottom of the cup, with thickness

δ˜Ek^{1 / 2}

(where Ek is the Ekman number).

Within the rotating core of the fluid, the radial pressure gradient balances the centrifugal forces, yet in the Ekman layer at the bottom of the cup fluid moves more slowly (due to the no-slip condition) leading to lower centrifugal forces. As pressure is constant through the boundary layer, an excess pressure gradient drives an inwards boundary-layer flow (this produces the spiral patterns often observed in tea-leaves) and fluid is ultimately ejected from the boundary layer into the core region. This causes columns of rotating fluid in the inviscid core flow to shorten and widen, and hence rotate at a slower rate in order to conserve angular momentum. It is through this mechanism by which a cup of stirred tea returns to rest.

A complete description for the flow requires us to take account of the Stewartson boundary layers, of thickness

δ˜Ek^{1 / 4},

located along the side walls of the cup which act as a conduit for fluid to return to the Ekman layer at the cup bottom and hence complete the circuit. In fact, embedded within this layer lies a thinner transition region, of thickness

Ek^{1 / 3},

where vertical flow velocities are reduced to zero. In a highly non-linear regime where the change of rotation rate is substantial, resulting in a non-negligible Rossby number, the Stewartson layers can become detached from the side walls and propagate into the core flow.

References

• Greenspan, H.P. (1968), The Theory of Rotating Fluids, Cambridge University Press ISBN 0-521-05147-9
• Benton, E.R., Clark, A. (1974), Spin-Up, Annual Review of Fluid Mechanics, vol 6, pp. 257-280
• Stewartson, K. (1957), On almost rigid rotations, Journal of Fluid Mechanics, vol. 3, pp. 17-26