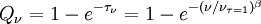To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
EmissivityThe emissivity of a material (usually written ε) is the ratio of energy radiated by the material to energy radiated by a black body at the same temperature. It is a measure of a material's ability to absorb and radiate energy. A true black body would have an ε = 1 while any real object would have ε < 1. Emissivity is a numerical value and does not have units. Product highlight
ExplanationThis emissivity depends on factors such as temperature, emission angle, and wavelength. A typical engineering assumption is to assume that a surface's spectral emissivity and absorptivity do not depend on wavelength, so that the emissivity is a constant. This is known as the grey body assumption. When dealing with non-black surfaces, the deviations from ideal black body behavior are determined by both the geometrical structure and the chemical composition, and follow Kirchhoff's law of thermal radiation: emissivity equals absorptivity (for an object in thermal equilibrium), so that an object that does not absorb all incident light will also emit less radiation than an ideal black body. Emissivity of earth's atmosphereThe emissivity of Earth's atmosphere varies according to cloud cover and the concentration of gases that absorb and emit energy in the thermal infrared (i.e., wavelengths around 8 to 14 micrometres). These gases are often called greenhouse gases, from their role in the greenhouse effect. The main naturally-occurring greenhouse gases are water vapor, carbon dioxide, methane, and ozone. The major constituents of the atmosphere, N2 and O2, do not absorb or emit in the thermal infrared.
Astrophysical greybodyThe monochromatic flux density radiated by a greybody at frequency ν through solid angle dΩ is given by Fν = Bν(T)QνdΩ where Bν is the Planck function for a blackbody at temperature T and emissivity Qν. For a uniform medium of optical depth τν radiative transfer means that the radiation will be reduced by a factor e − τ giving . The optical depth is often approximated by the ratio of the emitting frequency to the frequency where τ=1 all raised to an exponent β. For cold dust clouds in the interstellar medium β is approximately two. Therefore Q becomes,
See alsoCategories: Thermodynamics | Electromagnetic radiation |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Emissivity". A list of authors is available in Wikipedia. |