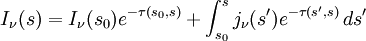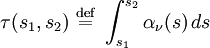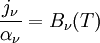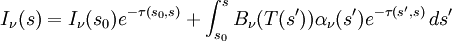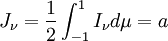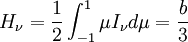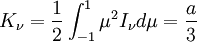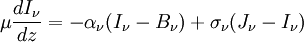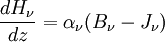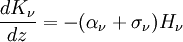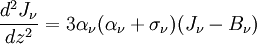To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Radiative transferThe term radiative transfer refers to the physical phenomena of energy transfer in the form of electromagnetic radiation. The propagation of radiation through a medium is affected by absorption, emission and scattering processes. The equation of radiative transfer describes these interactions mathematically. Equations of radiative transfer have application in wide variety of subjects; to mention a few -- satellite remote sensing, astronomy, optics, etc. Usually analytical solution of radiative transfer equation (RTE) does not exist in inhomogeneous 3D medium and must be solved by numerical methods. The work of Schuster (1905) [1] is probably the first paper discussing importance of multiple scattering in foggy atmosphere [2]. Product highlight
DefinitionsThe fundamental quantity which describes a field of radiation is the spectral intensity. If we think of a very small area element in the radiation field, there will be radiation energy flowing through that area element. The flow can be completely characterized by the amount of energy flowing per unit time per unit solid angle, the direction of the flow, and the wavelength interval being considered (polarization will be ignored for the moment). In terms of the spectral intensity, Iν, the energy flowing across an area element of area where θ is the angle that the unit direction vector The equation of radiative transferThe equation of radiative transfer simply says that as a beam of radiation travels, it loses energy to the atmosphere by absorption and gains energy by atmospheric emission, and redistributes energy by scattering. The differential form of the equation for radiative transfer is: where jν is the spectral emission coefficient which accounts for emission and scattering, αν is the spectral absorption coefficient, and σν is the scattering coefficient. The emission coefficient has units of energy/time/volume/solid angle/frequency. The amount of energy contributed by a volume element dV is The emission coefficient may be a function of the intensity if scattering occurs. The absorption coefficient α is the infinitesimal fraction by which the intensity is reduced as the beam travels an infinitesimal distance. It has units of 1/length and the fraction by which a beam's intensity is reduced when traveling a distance ds is just
Solutions to the equation of radiative transferSolutions to the equation of radiative transfer form an enormous body of work. The differences however, are essentially due to the various forms for the emission and absorption coefficients. If scattering is ignored, then a general solution in terms of the emission and absorption coefficients may be written: where τ(s1,s2) is the optical depth of the atmosphere between s1 and s2: Local thermodynamic equilibriumA particularly useful simplification of the equation of radiative transfer occurs under the conditions of local thermodynamic equilibrium (LTE). In this situation, the atmosphere consists of massive particles which are in equilibrium with each other, and therefore have a definable temperature. The radiation field is not, however in equilibrium and is being entirely driven by the presence of the massive particles. For an atmosphere in LTE, the emission coefficient and absorption coefficient are functions of temperature and density only, and are related by: where Bν(T) is the black body intensity at temperature T. The solution to the equation of radiative transfer is then: Knowing the temperature profile and the density profile of the atmospheric components will be enough to calculate a solution to the equation of radiative transfer. The Eddington approximationThe Eddington approximation can be used to obtain the intensity in a plane-parallel atmosphere with isotropic frequency-independent scattering. It assumes that the intensity is a linear function of μ = cosθ. i.e.
where z is the normal direction to the slab atmosphere. Note that expressing angular integrals in terms of μ simplifies things because dμ = − sinθdθ appears in the Jacobian of integrals in spherical coordinates. Extracting the first few moments of the intensity with respect to μ yields Thus the Eddington approximation is equivalent to setting Kν = 1 / 3Jν. Higher order versions of the Eddington approximation also exist, and consist of more complicated linear relations of the intensity moments. This extra equation can be used as a closure relation for the truncated system of moments. Note that the first two moments have simple physical meanings. Jν is the isotropic intensity at a point, and Hν is the flux through that point in the z direction. The radiative transfer through an isotropically scattering atmosphere at local thermal equilibrium is given by Integrating over all angles yields Premultiplying by μ, and then integrating over all angles gives Substituting in the closure relation, and differentiating with respect to z allows the two above equations to be combined to form the radiative diffusion equation This equation shows how the effective optical depth in scattering-dominated systems may be significantly different from that given by the scattering opacity if the absorptive opacity is small. See also
Further reading
References
Categories: Radiometry | Electromagnetic radiation |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Radiative_transfer". A list of authors is available in Wikipedia. |





 located at
located at 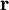 in time
in time 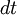 in the solid angle
in the solid angle 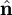 in the frequency interval
in the frequency interval 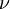 to
to 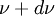 is
is
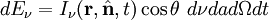
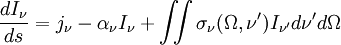
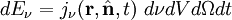
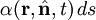 .
.