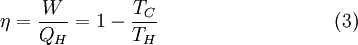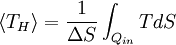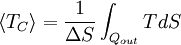To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Carnot cycleThe Carnot cycle is a particular thermodynamic cycle, modeled on the hypothetical Carnot heat engine, proposed by Nicolas Léonard Sadi Carnot in 1824 and expanded upon by Benoit Paul Émile Clapeyron in the 1830s and 40s. Every thermodynamic system exists in a particular state. A thermodynamic cycle occurs when a system is taken through a series of different states, and finally returned to its initial state. In the process of going through this cycle, the system may perform work on its surroundings, thereby acting as a heat engine. A heat engine acts by transferring energy from a warm region to a cool region of space and, in the process, converting some of that energy to mechanical work. The cycle may also be reversed. The system may be worked upon by an external force, and in the process, it can transfer thermal energy from a cooler system to a warmer one, thereby acting as a Heat Pump rather than a heat engine. The Carnot cycle is the most efficient cycle possible for converting a given amount of thermal energy into work or, conversely, for using a given amount of work for refrigeration purposes.
Product highlight
The Carnot cycleThe Carnot cycle when acting as a heat engine consists of the following steps:
Properties and significanceThe temperature-entropy diagram
The behavior of a Carnot engine or refrigerator is best understood by using a temperature-entropy (TS) diagram, in which the thermodynamic state is specified by a point on a graph with entropy (S) as the horizontal axis and temperature (T) as the vertical axis. For a simple system with a fixed number of particles, any point on the graph will represent a particular state of the system. A thermodynamic process will consist of a curve connecting an initial state (A) and a final state (B). The area under the curve will be: which is the amount of thermal energy transferred in the process. If the process moves to greater entropy, the area under the curve will be the amount of heat absorbed by the system in that process. If the process moves towards lesser entropy, it will be the amount of heat removed. For any cyclic process, there will be an upper portion of the cycle and a lower portion. For a clockwise cycle, the area under the upper portion will be the thermal energy absorbed during the cycle, while the area under the lower portion will be the thermal energy removed during the cycle. The area inside the cycle will then be the difference between the two, but since the internal energy of the system must have returned to its initial value, this difference must be the amount of work done by the system over the cycle. Mathematically, for a reversible process we may write the amount of work done over a cyclic process as: Since dU is an exact differential, its integral over any closed loop is zero and it follows that the area inside the loop on a T-S diagram is equal to the total work performed if the loop is traversed in a clockwise direction, and is equal to the total work done on the system as the loop is traversed in a counterclockwise direction. The Carnot cycle
Evaluation of the above integral is particularly simple for the Carnot cycle. The amount of energy transferred as work is The total amount of thermal energy transferred between the hot reservoir and the system will be and the total amount of thermal energy transferred between the system and the cold reservoir will be
The efficiency η is defined to be: where
This efficiency makes sense for a heat engine, since it is the fraction of the heat energy extracted from the hot reservoir and converted to mechanical work. It also makes sense for a refrigeration cycle, since it is the ratio of energy input to the refrigerator divided by the amount of energy extracted from the hot reservoir. Carnot's theoremIt can be seen from the above diagram, that for any cycle operating between temperatures TH and TC, none can exceed the efficiency of a Carnot cycle.
Carnot's theorem is a formal statement of this fact: No engine operating between two heat reservoirs can be more efficient than a Carnot engine operating between those same reservoirs. Thus, Equation 3 gives the maximum efficiency possible for any engine using the corresponding temperatures. A corollary to Carnot's theorem states that: All reversible engines operating between the same heat reservoirs are equally efficient. Rearranging the right side of the equation gives what may be a more easily understood form of the equation. Namely that the theoretical maximum efficiency of a heat engine equals the difference in temperature between the hot and cold reservoir divided by the absolute temperature of the hot reservoir. To find the absolute temperature in kelvins, add 273 degrees to the Celsius temperature. Looking at this formula an interesting fact becomes apparent. Lowering the temperature of the cold reservoir will have more effect on the ceiling efficiency of a heat engine than raising the temperature of the hot reservoir by the same amount. In the real world, this may be difficult to achieve since the cold reservoir is often an existing ambient temperature. In other words, maximum efficiency is achieved if and only if no new entropy is created in the cycle. Otherwise, since entropy is a state function, the required dumping of heat into the environment to dispose of excess entropy leads to a reduction in efficiency. So Equation 3 gives the efficiency of any reversible heat engine. Efficiency of real heat enginesCarnot realized that in reality it is not possible to build a thermodynamically reversible engine, so real heat engines are less efficient than indicated by Equation 3. Nevertheless, Equation 3 is extremely useful for determining the maximum efficiency that could ever be expected for a given set of thermal reservoirs. Although Carnot's cycle is an idealisation, the expression of Carnot efficiency is still useful. Consider the average temperatures, at which heat is input and output, respectively. Replace TH and TC in Equation (3) by <TH> and <TC> respectively. For the Carnot cycle, or its equivalent, <TH> is the highest temperature available and <TC> the lowest. For other less efficient cycles, <TH> will be lower than TH , and <TC> will be higher than TC. This can help illustrate, for example, why a reheater or a regenerator can improve thermal efficiency.
See also
References
Categories: Thermodynamic cycles | Atmospheric thermodynamics |
|||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Carnot_cycle". A list of authors is available in Wikipedia. | |||||||||||||||





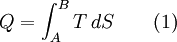
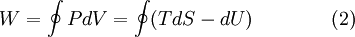
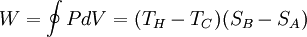
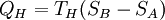
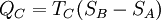 .
.