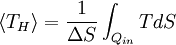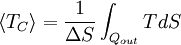To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Carnot heat engineA Carnot heat engine is a hypothetical engine that operates on the reversible Carnot cycle. The basic model for this engine was developed by Nicolas Léonard Sadi Carnot in 1824. The Carnot engine model was graphically expanded upon by Benoit Paul Émile Clapeyron in 1834 and mathematically elaborated upon by Rudolf Clausius in the 1850s and 60s from which the concept of entropy emerged. Every thermodynamic system exists in a particular state. A thermodynamic cycle occurs when a system is taken through a series of different states, and finally returned to its initial state. In the process of going through this cycle, the system may perform work on its surroundings, thereby acting as a heat engine. A heat engine acts by transferring energy from a warm region to a cool region of space and, in the process, converting some of that energy to mechanical work. The cycle may also be reversed. The system may be worked upon by an external force, and in the process, it can transfer thermal energy from a cooler system to a warmer one, thereby acting as a refrigerator rather than a heat engine. In the adjacent diagram, from the original 1824 paper by Sadi Carnot entitled On the Motive Power of Fire, we are told to “imagine two bodies A and B, kept each at a constant temperature, that of A being higher than that of B. These two bodies, to which we can give or from which we can remove the heat without causing their temperatures to vary, exercise the functions of two unlimited reservoirs of caloric. We shall call the first the furnace and the second the refrigerator.”[1] Carnot then explains how we can obtain motive power, i.e. “work”, by carrying a certain quantity of heat from the body A to the body B. Product highlight
Modern diagramAbove, we see the original piston-and-cylinder diagram used by Carnot in discussing his ideal engine; below, we see the Carnot engine as is typically modeled in current use: In the diagram shown, the “working body” (system), a term introduced by Clausius in 1850, can be any fluid or vapor body through which heat Q can be introduced or transmitted through to produce work. Carnot had postulated that the fluid body could be any substance capable of expansion, such as vapor of water, vapor of alcohol, vapor of mercury, a permanent gas, or air, etc. Although, in these early years, engines came in a number of configurations, typically QH was supplied by a boiler, wherein water was boiled over a furnace; QC was typically a stream of cold flowing water in the form of a condenser located on a separate part of the engine. The output work W here is the movement of the piston as it is used to turn a crank-arm, which was then typically used to turn a pulley so to lift water out of flooded salt mines. Carnot defined work as “weight lifted through a height”. Carnot's theoremIt can be seen from the above diagram, that for any cycle operating between temperatures TH and TC, none can exceed the efficiency of a Carnot cycle.
Carnot's theorem is a formal statement of this fact: No engine operating between two heat reservoirs can be more efficient than a Carnot engine operating between the same reservoirs. Thus, Equation 3 gives the maximum efficiency possible for any engine using the corresponding temperatures. A corollary to Carnot's theorem states that: All reversible engines operating between the same heat reservoirs are equally efficient. In other words, maximum efficiency is achieved if and only if no new entropy is created in the cycle. Otherwise, since entropy is a state function, the required dumping of heat into the environment to dispose of excess entropy leads to a reduction in efficiency. So Equation 3 gives the efficiency of any reversible heat engine. Efficiency of real heat enginesCarnot realised that in reality it is not possible to build a thermodynamically reversible engine, so real heat engines are less efficient than indicated by Equation 3. Nevertheless, Equation 3 is extremely useful for determining the maximum efficiency that could ever be expected for a given set of thermal reservoirs. Although Carnot's cycle is an idealisation, the expression of Carnot efficiency is still useful. Consider the average temperatures, at which heat is input and output, respectively. Replace TH and TC in Equation (3) by <TH> and <TC> respectively. For the Carnot cycle, or its equivalent, <TH> is the highest temperature available and <TC> the lowest. For other less efficient cycles, <TH> will be lower than TH , and <TC> will be higher than TC. This can help illustrate, for example, why a reheater or a regenerator can improve thermal efficiency.
Notes
References
See also |
|||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Carnot_heat_engine". A list of authors is available in Wikipedia. |