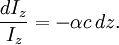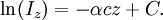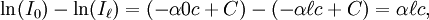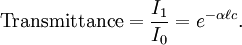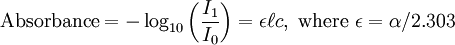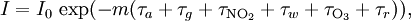To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Beer-Lambert lawIn optics, the Beer-Lambert law, also known as Beer's law or the Lambert-Beer law or the Beer-Lambert-Bouguer law (in fact, most of the permutations of these three names appear somewhere in literature) is an empirical relationship that relates the absorption of light to the properties of the material through which the light is travelling. Product highlight
Equations
There are several ways in which the law can be expressed,
where, Here,
In essence, the law states that there is a logarithmic dependence between the transmission of light through a substance and the concentration of the substance, and also between the transmission and the length of material that the light travels through. Thus if The units of absorber concentration ( If the material is a liquid, it is usual to express the absorber concentration as a mole fraction i.e. a dimensionless fraction. The units of the absorption coefficient are thus reciprocal length (e.g. cm−1). If the concentration is expressed in moles per unit volume, In the case of a gas, the concentration may be expressed as a number density (e.g. cm−3), in which case The value of the absorption coefficient In spectroscopy and spectrophotometry, the law is almost always defined in terms of common logarithm. In optics, the law is often defined in an alternate exponential form, The values of In molecular absorption spectrometry, the absorption coefficient α' is expressed in terms of a linestrength, S, and an (area-normalized) lineshape function, Φ. The frequency scale in molecular spectroscopy is often in cm-1, wherefore the lineshape function is expressed in units of 1/cm-1, which can look funny but is strictly correct. Since c is given as a number density in units of 1/cm3, the linestrength is often given in units of cm2cm-1/molecule. A typical linestrength in one of the vibrational overtone bands of smaller molecules, e.g. around 1.5 μm in CO or CO2, is around 10-23 cm2cm-1, although it can be larger for species with strong transitions, e.g. C2H2. The linestrengths of various transitions can be found in large databases, e.g. HITRAN. The lineshape function often takes a value around a few 1/cm-1, up to around 10/cm-1 under low pressure conditions, when the transition is Doppler broadened, and below this under atmospheric pressure conditions, when the transition is collision broadened. It has also become commonplace to express the linestrength in units of cm-2/atm since then the concentration is given in terms of a pressure in units of atm. A typical linestrength is then often in the order of 10-3 cm-2/atm. Under these conditions, the detectability of a given technique is often quoted in terms of ppm•m. The law tends to break down at very high concentrations, especially if the material is highly scattering. If the light is especially intense, nonlinear optical processes can also cause variances. DerivationAssume that particles may be described as having an area, α, perpendicular to the path of light through a solution, such that a photon of light is absorbed if it strikes the particle, and is transmitted if it does not. Define z as an axis parallel to the direction that photons of light are moving, and A and dz as the area and thickness (along the z axis) of a 3-dimensional slab of space through which light is passing. We assume that dz is sufficiently small that one particle in the slab cannot obscure another particle in the slab when viewed along the z direction. The concentration of particles in the slab is represented by c. It follows that the fraction of photons absorbed when passing through this slab is equal to the total opaque area of the particles in the slab, αAc dz, divided by the area of the slab, or αc dz. Expressing the number of photons absorbed by the slab as dIz, and the total number of photons incident on the slab as Iz, the fraction of photons absorbed by the slab is given by The solution to this simple differential equation is obtained by integrating both sides to obtain Iz as a function of z For a slab of real thickness, ℓ, the difference in light intensity I0 at z = 0, and I1 at z = ℓ, is given by or It is instructive to consider the consequences of error in an assumption that is implicit in this derivation, namely that every absorbing particle behaves independently with respect to the light. Error is introduced when particles interact by lying along the same optical path such that some particles are in the shadow of others. The assumption approaches accuracy only in very dilute solutions, and it becomes increasingly inaccurate with increasingly concentrated solutions or long optical paths. In practice, the accuracy of the assumption is better than the accuracy of most spectroscopic measurements up to an absorbance of 1 (or : I1 / I0 = 0.1) and to a good approximation, measurements of absorbance in this range are linearly related to the concentration of absorbing substances in solution. At higher absorbances, concentrations will be underestimated due to this shadow effect unless one employs a nonlinear relationship between absorbance and concentration. Beer-Lambert law in the atmosphereThis law is also applied to describe the attenuation of solar or stellar radiation as it travels through the atmosphere. In this case, there is scattering of radiation as well as absorption. The Beer-Lambert law for the atmosphere is usually written where each τx is the optical depth whose subscript identifies the source of the absorption or scattering it describes:
m is the optical mass or airmass factor, a term approximately equal (for small and moderate values of θ) to 1 / cos(θ), where θ is the observed object's zenith angle (the angle measured from the direction perpendicular to the Earth's surface at the observation site). This equation can be used to retrieve τa, the aerosol optical thickness, which is necessary for the correction of satellite images and also important in accounting for the role of aerosols in climate. HistoryThe law was discovered by Pierre Bouguer before 1729. It is often mis-attributed to Johann Heinrich Lambert, who cited Bouguer's “Essai d'Optique sur la Gradation de la Lumiere” (Claude Jombert, Paris, 1729) — and even quoted from it — in his “Photometria” in 1760. Much later, August Beer extended the exponential absorption law in 1852 to include the concentration of solutions in the absorption coefficient. See also
Categories: Spectroscopy | Electromagnetic radiation |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Beer-Lambert_law". A list of authors is available in Wikipedia. |





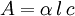
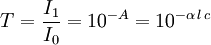
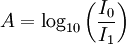
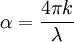
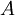 is the
is the 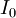 is the intensity of the incident light
is the intensity of the incident light
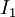 is the intensity after passing through the material
is the intensity after passing through the material
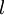 is the distance that the light travels through the material (the
is the distance that the light travels through the material (the 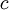 is the
is the 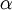 is the
is the 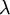 is the wavelength of the light
is the wavelength of the light
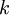 is the extinction coefficient
is the extinction coefficient
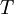 is the
is the 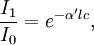
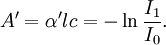
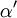 and
and 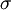 and represents the "true" cross section of the absorber (as can be seen from the derivation below). Therefore, care must be taken when interpreting data that the correct form of the law is used.
and represents the "true" cross section of the absorber (as can be seen from the derivation below). Therefore, care must be taken when interpreting data that the correct form of the law is used.