To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Ferromagnetic superconductor
Product highlight
The nature of the superconducting state in ferromagnetic superconductors is currently under debate. Early investigations [3] studied the coexistence of conventional s-wave superconductivity with itinerant ferromagnetism. However, the scenario of spin-triplet pairing soon gained the upper hand [4], [5]. Recently, a mean-field model for coexistence of spin-triplet pairing and ferromagnetism was developed by Nevidomskyy [6], and further studied by Linder and Sudbø [7]. It should be mentioned that we are here considering the situation of uniform coexistence of ferromagnetism and superconductivity. Another scenario where there is an interplay between magnetic and superconducting order in the same material is superconductors with spiral or helical magnetic order. Examples of such include ErRh4B4 and HoMo6S8. In these cases, the superconducting and magnetic order parameters entwine each other in a spatially modulated pattern, which allows for their mutual coexistence, although it is no longer uniform. Even spin-singlet pairing may coexist with ferromagnetism in this manner. TheoryIn conventional superconductors, the electrons constituting the Cooper pair have opposite spin, forming so-called spin-singlet pairs. However, other types of pairings are also permitted by the governing Pauli-principle. In the presence of a magnetic field, spins tend to align themselves with the field, which means that a magnetic field is detrimental for the existence of spin-singlet Cooper pairs. A viable mean-field Hamiltonian for modelling itinerant ferromagnetism coexisting with a non-unitary spin-triplet state may after diagonalization be written as [8], [9]:
ReferencesExperimental papers: Theoretical papers: |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Ferromagnetic_superconductor". A list of authors is available in Wikipedia. |





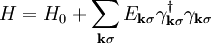 ,
,
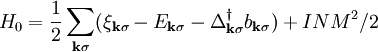 ,
,
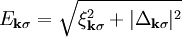 .
.


