Frank-Read Source

A Frank-Read Source is a mechanism explaining the generation of multiple dislocations in specific well spaced slip planes in crystals when they are deformed. It was proposed by and named after Sir Charles Frank and Thornton Read. When a crystal is deformed slip is found to occur only on certain well spaced slip planes. Furthermore, it is found that in order for that slip to occur dislocations must be generated in the material. This implies that during deformation dislocations must be primarily generated in these planes. The Frank-Read Source is a mechanism to explain this phenomena.

Additional recommended knowledge

Don't let static charges disrupt your weighing accuracy

Daily Sensitivity Test

How to quickly check pipettes?

History

Sir Charles Frank detailed the history of the discovery from his perspective in the Proceedings of the Royal Society of London in 1980.^[1]. In 1950 Sir Charles Frank , who was then a research fellow in the physics department at the University of Bristol, visited the United States to participate in a conference on crystal plasticity in Pittsburgh. Sir Charles Frank arrived in the United States well in advance of the conference to spend time at a naval laboratory and to give a lecture at Cornell University. When during his travels in Pennsylvania Sir Charles Frank visited Pittsburgh he received a letter from a fellow scientist Jock Eshelby suggesting that he read a recent paper by Gunther Leibfried. Sir Charles Frank was supposed to board a train to Cornell to give his lecture at Cornell, but before departing for Cornell he went to the library at Carnegie Mellon to obtain a copy of the paper. The library did not yet have the journal with Leibfried's paper but the staff at the library believed that the journal could be in the recently arrived package from Germany. Sir Charles Frank decided to wait for the library to open the package which did indeed contain the journal. Upon reading the paper he took a train to Cornell where he was told to pass the time until 5:00 as the faculty was in meeting. Sir Charles Frank decided to take a walk between 3:00 and 5:00. During those two hours while considering the Leibfried paper he formulated the theory for what was later named the Frank-Read source. A couple of days later he traveled to the conference on crystal plasticity in Pittsburgh where he ran into Thorton Read in the Hotel lobby. Upon encountering each other the two scientist immediately discovered that they had come-up with the same idea for dislocation generation almost simultaneously, Sir Charles Frank during his walk at Cornell and Thorton Read during tea the previous Wednesday, and decided to write a joint paper on the topic. The mechanism for dislocation generation described in that paper is now known as the Frank Read source. Sir Charles Frank's rendition of this story, on which this summary is based, is a far more engaging read which should be read for a more complete picture.

Mechanism^{[2] [3]}.

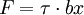The Frank Read Source is mechanism based on dislocation multiplication in a slip plane under shear stress. Consider a straight dislocation in a crystal slip plane with its two ends, A and B, pinned. If a shear stress τ is exerted on the slip plane a force , where b is the burgers vector of the dislocation and x is the distance between the pinning sites a and b, is exerted on the dislocation line as a result of the shear stress. This force acts perpendicular to the line inducing the dislocation to lengthen and curve into an arc. The bending force caused by the shear stress is opposed by the line tension of the dislocation which acts on each end of the dislocation along the direction of dislocation line away from a and b with a magnitude of 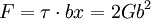Gb² where G is the Shear modulus. If the dislocation bends, the ends of the dislocation make an angle with the horizontal between a and b which gives the line tensions acting along the ends a vertical component acting directly against the force induced by the shear stress. If sufficient shear stress is applied and the dislocation bends, the vertical component from the line tensions, which acts directly against the force caused by the shear stress, grows as the dislocation approaches a semicircular shape. When the dislocation becomes a semicircle all of the line tension is acting against the bending force induced by the shear stress because the line tension is perpendicular to the horizontal between a and b. For the dislocation to reach this point, it is thus evident that must be satisfied and from which we can solve for the shear stress: 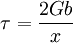. This is the stress required to generate dislocation from a Frank Read source. If the shear stress increases any further and the dislocation passes the semicircular equilibrium state, it will spontaneously continue to bend and grow spiraling around the a and b pinning points until the segments spiraling around the A and B pinning points collide and cancel. The process results in a dislocation loop around A and B in the slip plane which expands under continued shear stress and also in a new dislocation line between A and B which under renewed or continued shear can continue to generate dislocation loops in the manner just described. A Frank Read Loop can thus generate many dislocations in a plane in a crystal under applied stress. The Frank Read source mechanism explains why dislocations are primarily generated on certain slip planes;dislocations are primarily generated in just those planes with Frank Read sources. It is important to note that if the shear stress does not exceed and the dislocation does not bend past the semicircular equilibrium state it will not form a dislocation loop and simply revert to its original state.

References