To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Gas Dynamics Shocks
Product highlightExplanation of phenomenaShock is formed due to coalescing (coming together) of various small pressure pulses. Sounds waves are pressure wave and it is at the speed of the sound wave the disturbances are communicated in the medium. When an object is moving in a flow field the object sends out disturbances which propagate at the speed of sound and adjusts the remaining flow field accordingly. However, if the object itself happens to travel at speed greater than sound, then the disturbances created by the object would not have traveled and communicated to the rest of the flow field and this results in an abrupt change of property, which is termed as shock in gas dynamics terminology. Shocks are characterized by discontinuities changes in flow properties such as velocity, pressure, temperature etc. Typically shock thickness is of a few mean free paths (of the order of 10 -8 m). Shocks are irreversible occurrence (Non-Isentropic) in supersonic flows. Normal Shock formulas
Note : '1' refers to upstream properties '2' refers to down stream properties subscript '0' - refers to Total or stagnation properties T refers to Temperature M refers to Mach number P refers to Density
γ is the ratio of the specific heats |
||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Gas_Dynamics_Shocks". A list of authors is available in Wikipedia. |





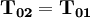
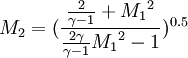
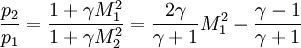
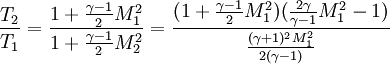
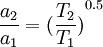
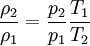
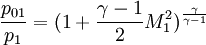
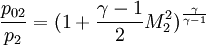
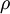 refers to Density
refers to Density


