To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Gibbs-Thomson effectThe Gibbs-Thomson effect (not to be confused with the Thomson effect) relates surface curvature to vapor pressure and chemical potential. It is named after Josiah Willard Gibbs and three Thomsons: James Thomson, William Thomson, 1st Baron Kelvin, and Sir Joseph John Thomson. Product highlightIt leads to the fact that small liquid droplets (i.e. particles with a high surface curvature) exhibit a higher effective vapor pressure, since the surface is larger in comparison to the volume. The Gibbs-Thomson effect can cause strong depression of the freezing point of liquids dispersed within fine porous materials. Another notable example of the Gibbs-Thomson effect is Ostwald ripening, in which concentration gradients cause small precipitates to dissolve and larger ones to grow. The Gibbs-Thomson equation for a precipitate with radius R is:
Ostwald ripening is thought to occur in the formation of orthoclase megacrysts in granites as a consequence of subsolidus growth. See rock microstructure for more. |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Gibbs-Thomson_effect". A list of authors is available in Wikipedia. |





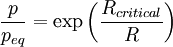
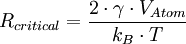
 m
m

