To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Heegaard splittingIn the mathematical field of geometric topology, a Heegaard splitting is a decomposition of a compact oriented 3-manifold that results from dividing it into two handlebodies. The importance of Heegaard splittings has grown in recent years as more connections and applications have been found. Product highlight
DefinitionsLet V and W be handlebodies of genus g, and let f be a homeomorphism from the boundary of V to the boundary of W. By gluing V to W along f we obtain the compact oriented 3-manifold It is a deep fact that every closed, orientable three-manifold may be obtained in this manner. This follows from deep results on the triangulability of three-manifolds due to Moise. This contrasts strongly with higher dimensional manifolds which need not admit smooth or piecewise linear structures. The decomposition of M into two handlebodies is called a Heegaard splitting, and their common boundary H is called the Heegaard surface of the splitting. Splittings are considered up to isotopy. The gluing map f need only be specified up to taking a double coset in the mapping class group of H. This connection with the mapping class group was first made by W. R. Lickorish. Heegaard splittings can also be defined for compact 3-manifolds with boundary by replacing handlebodies with compression bodies. The gluing map is between the positive boundaries of the compression bodies. A simple closed curve on a surface is essential if it is does not bound a disc on the surface. A Heegaard splitting is reducible if there is an essential simple closed curve α on H which bounds a disk in both V and in W. A splitting is irreducible if it is not reducible. It follows from Haken's Lemma that in a reducible manifold every splitting is reducible. A Heegaard splitting is stabilized if there are essential simple closed curves α and β on H where α bounds a disk in V, β bounds a disk in W, and α and β intersect exactly once. It follows from Waldhausen's Theorem that every reducible splitting of an irreducible manifold is stabilized. A Heegaard splitting is weakly reducible if there are disjoint essential simple closed curves α and β on H where α bounds a disk in V and β bounds a disk in W. A splitting is strongly irreducible if it is not weakly reducible. A Heegaard splitting is minimal or minimal genus if there is no other splitting of the ambient three-manifold of lower genus. The minimal value g of the splitting surface is the Heegaard genus of M. Generalized Heegaard splittingsA generalized Heegaard splitting of M is a decomposition into compression bodies A generalized Heegaard splitting is called strongly irreducible if each There is an analogous notion of thin position, defined for knots, for Heegaard splittings. The complexity of a connected surface S, c(S), is defined to be ExamplesThree-sphere: Recall that the three-sphere S3 is the set of vectors in Under the usual identification of Stabilization: Given an Heegaard splitting H in M the stabilization of H is formed by taking the connected sum of the pair (M,H) with the pair (S3,T2). It is easy to show that the stabilization procedure yields stabilized splittings. Inductively, a splitting is standard if it is the stabilization of a standard splitting. Lens spaces: All have a standard splitting of genus one. This is the image of the Clifford torus in S3 under the quotient map used to define the lens space in question. It follows from the structure of the mapping class group of the two-torus that only lens spaces have splittings of genus one. Three-torus: Recall that the three-torus T3 is the Cartesian product of three copies of S1 (circles). Let x0 be a point of S1 and consider the graph
TheoremsAlexander's Lemma: Up to isotopy, there is a unique (piecewise linear) embedding of the two-sphere into the three-sphere. (In higher dimensions this is known as the Schoenflies Theorem. In dimension two this is the Jordan curve Theorem.) This may be restated as follows: the genus zero splitting of S3 is unique. Waldhausen's Theorem: Every splitting of S3 is obtained by stabilizing the unique splitting of genus zero. Suppose now that M is a closed orientable three-manifold. Reidemeister-Singer Theorem: For any pair of splittings H1 and H2 in M there is a third splitting H in M which is a stabilization of both. Haken's Lemma: Suppose that S1 is an essential two-sphere in M and H is a Heegaard splitting. Then there is an essential two-sphere S2 in M meeting H in a single curve. ClassificationsThere are several classes of three-manifolds where the set of Heegaard splittings is completely known. For example, Waldhausen's Theorem shows that all splittings of S3 are standard. The same holds for lens spaces (as proven by Francis Bonahon and J.P. Otal). Splittings of Seifert fiber spaces are more subtle. Here, all splittings may be isotoped to be vertical or horizontal (as proven by Yoav Moriah and Jennifer Schultens). Splittings of torus bundles (which includes all three-manifolds with Sol geometry) have been classified by Daryl Cooper and Martin Scharlemann. It follows from their work that all torus bundles have a unique splitting of minimal genus. All other splittings of the torus bundle are stabilizations of the minimal genus one. Outside of a few special cases, as of 2005, little is known about the set of splittings of closed hyperbolic three-manifolds. Applications and connectionsMinimal surfacesHeegaard splittings appeared in the theory of minimal surfaces first in the work of Blaine Lawson who proved that embedded minimal surfaces in compact manifolds of positive sectional curvature are Heegaard splittings. This result was extended by William Meeks to flat manifolds, except he proves that an embedded minimal surface in a flat three-manifold is either a Heegaard surface or totally geodesic. Meeks and S. T. Yau went on to use results of Waldhausen to prove results about the topological uniqueness of minimal surface of finite topology in R3. The final topological classification of embedded minimal surfaces in R3 was given by Meeks and Frohman. The result relied heavily on techniques developed for studying the topology of Heegaard splittings. Heegaard Floer homologyHeegaard diagrams, which are simple combinatorial descriptions of Heegaard splittings, have been used extensively to construct invariants of three-manifolds. The most recent example of this is the Heegaard Floer homology of Peter Ozsvath and Zoltán Szabó. The theory uses the gth symmetric product of a Heegaard surface as the ambient space, and tori built from the boundaries of meridian disks for the two handlebodies as the Lagrangian submanifolds. HistoryThe idea of a Heegaard splitting was introduced by Poul Heegaard in his 1898 thesis and was perhaps inspired by what is known today as Morse theory. While Heegaard splittings were studied extensively by mathematicians such as Wolfgang Haken and Friedhelm Waldhausen in the 1960s, it was not until a few decades later that the field was rejuvenated by Casson and Gordon, primarily through their concept of strong irreducibility. The modern study of the topology of Heegaard splittings was pushed forward through the work of Hyam Rubinstein, Martin Scharlemann, Tsuyoshi Kobayashi, Kanji Morimoto, Makoto Sakuma, Abigail Thompson, Jennifer Schultens, Yoav Moriah, Francis Bonahon, J.P. Otal, Klaus Johannson and many others. See also
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Heegaard_splitting". A list of authors is available in Wikipedia. |





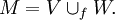
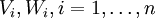 and surfaces
and surfaces 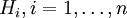 such that
such that 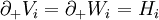 and
and 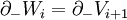 . The interiors of the compression bodies must be pairwise disjoint and their union must be all of
. The interiors of the compression bodies must be pairwise disjoint and their union must be all of 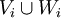 of
of 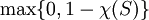 ; the complexity of a disconnected surface is the sum of complexities of its components. The complexity of a generalized Heegaard splitting is the multi-set {c(S_i)}, where the index runs over the Heegaard surfaces in the generalized splitting. These multi-sets can be well-ordered by lexicographical ordering (monotonically decreasing). A generalized Heegaard splitting is thin if its complexity is minimal.
; the complexity of a disconnected surface is the sum of complexities of its components. The complexity of a generalized Heegaard splitting is the multi-set {c(S_i)}, where the index runs over the Heegaard surfaces in the generalized splitting. These multi-sets can be well-ordered by lexicographical ordering (monotonically decreasing). A generalized Heegaard splitting is thin if its complexity is minimal.
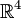 with length one. Intersecting this with the
with length one. Intersecting this with the 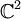 we may view
we may view 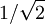 forms a Clifford torus,
forms a Clifford torus, 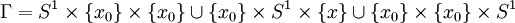 . It is an easy exercise to show that V, a regular neighborhood of
. It is an easy exercise to show that V, a regular neighborhood of 

