To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Hess's lawHess' Law is a law of physical chemistry named for Germain Hess's expansion of the Hess Cycle and used to predict the enthalpy change and conservation of energy (denoted as state function ΔH) regardless of the path through which it is to be determined. Product highlight
ExplanationThe law states that because enthalpy is a state function, the enthalpy change of a reaction is the same regardless of what pathway is taken to achieve the products. In other words, only the start and end states matter to the reaction, not the individual steps between. This allows the change in enthalpy for a reaction to be calculated even when it cannot be measured directly. This is accomplished by performing arithmetic operations on chemical equations. Chemical equations may be multiplied (or divided) by a whole number. When an equation is multiplied by a constant, its ΔH must be multiplied by the same number as well. If an equation is reversed, ΔH for the reaction must also be reversed (i.e. -ΔH). Addition of chemical equations can lead to a net equation. If enthalpy change is included for each equation and added, the result will be the enthalpy change for the net equation. If the net enthalpy change is negative (ΔHnet < 0), the reaction is more likely to be an exothermic reaction (positive ΔH yields endothermic reactions). (But entropy also plays an important role in determining spontaneity, so some reactions with positive enthalpy change are spontaneous anyway.) Hess's Law says that enthalpy changes are additive. Thus the ΔH for a single reaction can be calculated from the difference between the heat of formation of the products minus the heat of formation of the reactants. In mathematical terms:
For multiple reactions, the notation changes, but the concept remains the same:
UseIf one knows the ΔHf (Enthalpy change of formation) of both the reactants and the products one can deduce the enthalpy change of the reaction.
Hess' Law of constant heat summation states that the overall enthalpy change for a process depends only on the initial and final states of the system, and is independent of the route or pathway between these states. The same process can be used for information of enthalpy of combustions although the arrows in the illustration above would be pointing down. This has no effect except switching the signs of the enthalpies. This formula should be substituted:
Typical useTypical table for making a Hess cycle:
Using this ΔHfɵ data the ΔHcɵ for the below reaction can be found:
ExampleGiven: After the multiplication and reversing of the equations (and their enthalpy changes), the result is:
Adding these equations and canceling out the common terms on both sides, we get
The concepts of Hess's law can be expanded to include changes in entropy and in free energy. This application is especially helpful for these calculations because they cannot be measured directly, and therefore must be calculated using a limited number of ways. This is especially true of free energy, for which this method is one of only three basic ways to calculate Hess's law. For entropy:
For free energy:
|
|||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Hess's_law". A list of authors is available in Wikipedia. |





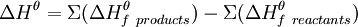 .
.
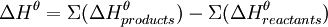 .
.


