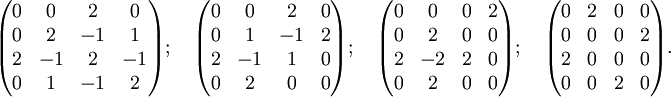Higher spin alternating sign matrix

In mathematics, a higher spin alternating sign matrix is a generalisation of the alternating sign matrix (ASM), where the columns and rows sum to an integer r (the spin) rather than simply summing to 1 as in the usual alternating sign matrix definition. HSASMs are square matrices whose elements may be integers in the range −r to +r. When traversing any row or column of an ASM or HSASM, the sign of each non-zero element alternates. Thus any matrix with two adjacent elements of the same sign is not an ASM.

Additional recommended knowledge

Weighing the right way

What is the Sensitivity of my Balance?

Better weighing performance in 6 easy steps

There does appear to be some variation in the accepted definition of the ASM, however. In some cases, the alternating element condition has been relaxed, which significantly increases the number of possible matrices.

High spin ASMs have found application in statistical mechanics and physics, where they have been found to represent symmetry groups in ice crystal formation.

Some typical examples of HSASMs are shown below:

The set of HSASMs is a superset of the ASMs. The extreme points of the convex hull of the set of r-spin HSASMs are themselves integer multiples of the usual ASMs.