To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Square-lattice Ising modelThe two-dimensional square-lattice Ising model was solved by Lars Onsager in 1944 for the special case that the external field H = 0. The general case for Consider the 2D Ising model on a square lattice Λ with N sites, with periodic boundary conditions in both the horizontal and vertical directions, which effectively reduces the geometry of the model to a torus. In a general case, the horizontal coupling J is not equal to the coupling in the vertical direction, J*. With an equal number of rows and columns in the lattice, there will be N of each. In terms of
where β = 1 / (kT) where T is absolute temperature and k is Boltzmann's constant, the partition function ZN(K,L) is given by Product highlight
Dual latticeConsider a configuration of spins {σ} on the square lattice Λ. Let r and s denote the number of unlike neighbours in the vertical and horizontal directions respectively. Then the summand in ZN corresponding to {σ} is given by
Construct a dual lattice ΛD as depicted in the diagram. For every configuration {σ}, a polygon is associated to the lattice by drawing a line on the edge of the dual lattice if the spins separated by the edge are unlike. Since by traversing a vertex of λ the spins need to change an even number of times so that one arrives at the starting point with the same charge, every vertex of the dual lattice is connected to an even number of lines in the configuration, defining a polygon. This reduces the partition function to summing over all polygons in the dual lattice, where r and s are the number of horizontal and vertical lines in the polygon, with the factor of 2 arising from the inversion of spin configuration. Low-temperature expansionAt low temperatures, K, L approach infinity, so that as defines a low temperature expansion of ZN(K,L). High-temperature expansionSince
Therefore where v = tanhK and w = tanhL. Since there are N horizontal and vertical edges, there are a total of 22N terms in the expansion. Every term corresponds to a configuration of lines of the lattice, by associating a line connecting i and j if the term vσiσj (or wσiσj) is chosen in the product. Summing over the configurations, using shows that only configurations with an even number of lines at each vertex (polygons) will contribute to the partition function, giving where the sum is over all polygons in the lattice. Since tanh K, tanh L The two expansions can be related using the Kramers-Wannier duality. References
Categories: Statistical mechanics | Lattice models |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Square-lattice_Ising_model". A list of authors is available in Wikipedia. |


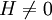 has yet to be found.
has yet to be found.
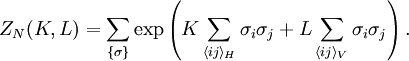



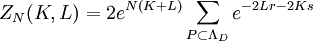
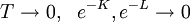 , so that
, so that
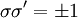 one has
one has
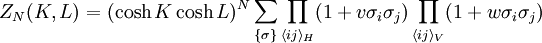
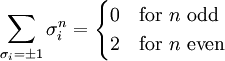
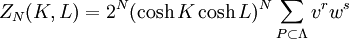
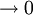 as
as 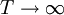 , this gives the high temperature expansion of
, this gives the high temperature expansion of 

