Kramers-Wannier duality

The Kramers-Wannier duality is a symmetry in statistical physics. It relates the free energy of a two-dimensional square-lattice Ising model at a low temperature to that of another Ising model at a high temperature. It was discovered by Hendrik Kramers and Gregory Wannier in 1941. With the aid of this duality Kramers and Wannier found the exact location of the critical point for the Ising model on the square lattice.

Additional recommended knowledge

Guide to balance cleaning: 8 simple steps

Daily Visual Balance Check

Daily Sensitivity Test

Similar dualities establish relations between free energies of other statistical models. For instance, in 3 dimensions the Ising model is dual to an Ising gauge model.

Derivation

The low temperature expansion for $(K *, L *)$ is

$Z_N(K^*,L^*) = 2 e^{N(K^*+L^*)} \sum_{ P \subset \Lambda_D} (e^{-2L^*})^r(e^{-2K^*})^s$

which by using the transformation

$\tanh K = e^{-2L*}, \ \tanh L = e^{-2K*}$

gives

$Z_N(K^*,L^*) = 2(\tanh K \; \tanh L)^{-N/2} \sum_{P} v^r w^s$

$= 2(\sinh 2K \; \sinh 2L)^{-N/2} Z_N(K,L)$

where $v = tanh K$ and $w = tanh L$ , yielding a relation with the high-temperature expansion.

The relations can written more symmetrically as

sinh2 K * sinh2 L = 1

sinh2 L * sinh2 K = 1

With the free energy per site in the thermodynamic limit

$f(K,L) = \lim_{N \rightarrow \infty} f_N(K,L) = -kT \lim_{N\rightarrow \infty} \frac{1}{N} \log Z_N(K,L)$

the Kramers-Wannier duality gives

$f(K^*,L^*) = f(K,L) + \frac{1}{2} kT \log(\sinh 2K \sinh 2L)$

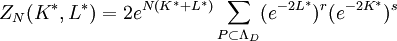
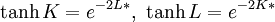
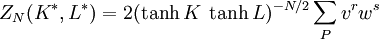
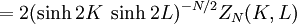
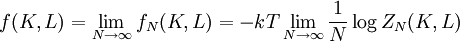
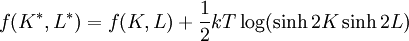
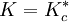In the isotropic case where K = L, if there is a critical point at $K = K c$ , then there is another at $K = K_c^*$ . Hence, in the case of there being a unique critical point, it would be located at 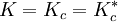$K = K_c = K_c^*$ , implying $sinh2 K c = 1$ , yielding $k T c = 2.2692 J$

References

H. A. Kramers and G. H. Wannier (1941). "Statistics of the two-dimensional ferromagnet". Physical Review 60: 252-262.
J. B. Kogut (1979). "An introduction to lattice gauge theory and spin systems". Reviews of Modern Physics 51: 659-713.

Categories: Statistical mechanics | Lattice models