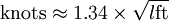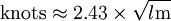Hull speed

Hull speed, sometimes referred to as displacement speed, is a common rule of thumb based on the speed/length ratio of a displacement hull, used to provide the approximate speed potential (i.e. maximum speed possible) of the hull. It is the speed of a deep water wave whose wavelength is equal to the waterline length of the hull. The most commonly used hull speed constant is the wave propagation speed for the hull length, and it serves well for traditional sailing hulls. In English units, it is expressed as:

Or, in metric units:

where "l" is the length of the waterline (LWL) in feet or meters.

Hull speed is typically not a term used by naval architects (they use, instead, a specific speed/length ratio for the hull in question) but is often used by amateur builders of displacement hulls, such as small sailboats and rowboats.

The concept has to do with the effect of drag from the water on the hull. With all else being equal, a longer boat will have a higher hull speed. In yacht racing this is demonstrated by looking at handicap ratings such as PHRF; generally speaking longer boats have higher handicap, although there are other factors.

Additional recommended knowledge

Weighing the right way

Better weighing performance in 6 easy steps

How to ensure accurate weighing results every day?

History

The quantification of the speed/length ratio is generally credited to William Froude, who used a series of scale models to measure the resistance each model offered when towed at a given speed. Froude's observations led him to derive the Froude number, which allows experimental observations performed on scale models to be applied to full-scale vessels.

The speed-to-length ratio is traditionally expressed in knots of speed (V) and feet of waterline length (LWL):

Use

The speed/length ratio is strictly only useful when comparing different scalings of otherwise identical hulls whose drag is dominated by wave drag. However, for many hulls, a generic speed/length ratio will provide a good general estimate of the speed potential of the hull when it is operating in displacement mode. This is commonly called the hull speed, and this term is commonly found in the boating community and among amateur builders, though it is not used by naval architects or engineers.

The hull speed limit does not readily apply to certain types of hull which are not primarily limited by wave drag. Examples of these craft are:

• Very long, narrow hulls such as rowing shells, flatwater racing canoes and kayaks, and multihulls such as catamarans and proas. In these hulls, skin drag is often far greater at the normal operating speeds than the wave drag.
• Boats which operate in a semi-displacement mode where the hull shape provides some lift. In these hulls, the lift reduces the displacement, providing a reduction in the quantity of water moved and a corresponding reduction in wave drag.
• Small, highly powered boats such as sailing dinghies and personal watercraft, which can easily plane. These hulls quickly and easily surmount their bow waves, and rely entirely on dynamic lift when planing.

Some boats, such as the proa, have both a narrow hull and are capable of operating in a semi-displacement or planing mode. Very large vessels, such as supertankers, are also generally limited by skin drag. This is not due to any special property of the hull, but rather to a low power to displacement ratio, which keeps the vessels operating at speed/length ratios well below the hull speed.

The most commonly used hull speed constant is the wave propagation speed for the hull length, and it serves well for traditional sailing hulls. In English units, it is expressed as:

Or, in metric units:

In reality, speed/length ratios (in English units) of real hulls vary from as low as 1.18 for blunt hulls such as barges to over 1.42 for long, thin hulls. Also, since hull speed takes into account only the wave making resistance, large hulls (over 200 ft or 60 m) will be more limited by other forms of drag[1].

Examples

Displacement hulls (for example those not planing on the surface of the water) have a maximum speed beyond which they tend to 'dig in', with their bows high and sterns low, and become increasingly wasteful of propulsive power. This is known as their hull speed and it depends mainly upon waterline length. For various displacement boat hulls the following table relates waterline lengths to hull speeds and so gives some examples of usage of the unit knots..

References

• A simple explanation of hull speed as it relates to heavy and light displacement hulls
• Hull speed chart for use with rowed boats
• On the subject of high speed monohulls, Daniel Savitsky, Professor Emeritus, Davidson Laboratory, Stevens Institute of Technology
• Low Drag Racing Shells