To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Importance samplingImportance sampling is a general technique for estimating the properties of a particular distribution, while only having samples generated from a different distribution than the distribution of interest. Depending on the application, the term may refer to the process of sampling from this alternative distribution, the process of inference, or both. Product highlight
Basic theoryMore formally, let X be a random variable in S. Let p be a probability measure on S, and f some function on S. Then the expectation of f under p can be written as
If we have random samples In that case, we can easily obtain the Monte-Carlo empirical estimate of
Unfortunately, when the samples are generated from a different distribution than the one that we are interested in, we can no longer use this straightforward estimate. However, we may use the importance sampling technique, which consists of placing different importance on each sample, depending on how likely it was for it to have been generated by the distribution that we're interested in, p, rather than the actual sampling distribution, q. More formally, consider another probability measure, q, with the same support as p. From the definition of the expectation given above, we have
where
where The technique is completely general and the above analysis can be repeated essentially exactly also for other choices of p, for example when it represents a conditional distribution. Note that when p is the uniform distribution, we are just estimating the (scaled) integral of f over S, so the method can also be used for estimating simple integrals. There are two main applications of importance sampling methods, which naturally, are interrelated. While the aim of both applications is to estimate statistics of random variables, the field of probabilistic inference focuses more on the estimation of p or related statistics, while the field of simulation focuses more on the choice of the distribution q. Nevertheless, the basic theory and tools are identical. Application to probabilistic inferenceSuch methods are frequently used to estimate posterior densities or expectations in state and/or parameter estimation problems in probabilistic models that are too hard to treat analytically. Application to simulationImportance sampling (IS) is a variance reduction technique that can be used in the Monte Carlo method. The idea behind IS is that certain values of the input random variables in a simulation have more impact on the parameter being estimated than others. If these "important" values are emphasized by sampling more frequently, then the estimator variance can be reduced. Hence, the basic methodology in IS is to choose a distribution which "encourages" the important values. This use of "biased" distributions will result in a biased estimator if it is applied directly in the simulation. However, the simulation outputs are weighted to correct for the use of the biased distribution, and this ensures that the new IS estimator is unbiased. The weight is given by the likelihood ratio, that is, the Radon-Nikodym derivative of the true underlying distribution with respect to the biased simulation distribution. The fundamental issue in implementing IS simulation is the choice of the biased distribution which encourages the important regions of the input variables. Choosing or designing a good biased distribution is the "art" of IS. The rewards for a good distribution can be huge run-time savings; the penalty for a bad distribution can be longer run times than for a general Monte Carlo simulation without importance sampling. Mathematical ApproachConsider estimating by simulation the probability Importance sampling is concerned with the determination and use of an alternate density function where is a likelihood ratio and is referred to as the weighting function. The last equality in the above equation motivates the estimator This is the IS estimator of Now, the IS problem then focuses on finding a biasing density Conventional biasing methodsAlthough there are many kinds of biasing methods, the following two methods are most widely used in the applications of IS. ScalingShifting probability mass into the event region In IS by scaling, the simulation density is chosen as the density function of the scaled random variable and the weighting function is While scaling shifts probability mass into the desired event region, it also pushes mass into the complementary region TranslationAnother simple and effective biasing technique employs translation of the density function (and hence random variable) to place much of its probability mass in the rare event region. Translation does not suffer from a dimensionality effect and has been successfully used in several applications relating to simulation of digital communication systems. It often provides better simulation gains than scaling. In biasing by translation, the simulation density is given by where Effects of System ComplexityThe fundamental problem with IS is that designing good biased distributions becomes more complicated as the system complexity increases. Complex systems are the systems with long memory since complex processing of a few inputs is much easier to handle. This dimensionality or memory can cause problems in three ways:
In principle, the IS ideas remain the same in these situations, but the design becomes much harder. A successful approach to combat this problem is essentially breaking down a simulation into several smaller, more sharply defined subproblems. Then IS strategies are used to target each of the simpler subproblems. Examples of techniques to break the simulation down are conditioning and error-event simulation (EES) and regenerative simulation. Evaluation of ISIn order to identify successful IS techniques, it is useful to be able to quantify the run-time savings due to the use of the IS approach. The performance measure commonly used is Variance Cost FunctionVariance is not the only possible cost function for a simulation, and other cost functions, such as the mean absolute deviation, are used in various statistical applications. Nevertheless, the variance is the primary cost function addressed in the literature, probably due to the use of variances in confidence intervals and in the performance measure An associated issue is the fact that the ratio References
See also
References
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Importance_sampling". A list of authors is available in Wikipedia. |





![\mathbf{E}[f(X)|p] \equiv \int f(x) p(x) \,dx.](images/math/4/3/4/434c33fd63e19edafdb1a84b9974028d.png)
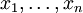 , generated according to
, generated according to
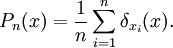
![\mathbf{E}[f(X)|p]](images/math/2/5/b/25b9ae502c9f9c910a6c8fd857566114.png)
![\hat{\mathbf{E}}_n[f] = \int f(x) P_n(x) \,dx = \frac{1}{n} \sum_{i=1}^n f(x_i).](images/math/8/9/f/89f39332d2c87934ed91ddb00738746f.png)
![\mathbf{E}[f(X)|p] = \frac{\int f(x) w(x) q(x) \,dx}{\int w(x) q(x) dx},](images/math/7/9/8/79849180aa3af23963947b4d1c1094f8.png)
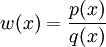 , is known as
the importance weight and the distribution
, is known as
the importance weight and the distribution ![\mathbf{E}[f(X)w(X)|q]](images/math/c/3/3/c33fb5b9679bd4c140f9a8a54ce1c6a8.png) and
and ![\mathbf{E}[w(X)|q]](images/math/1/7/5/1755172e962ec3c0fc6cc52ec6048a46.png) .
.
![\hat{\mathbf{E}}_{n,q}[f] = \frac{1/n \sum_{i=1}^n f(x_i) w(x_i)}{1/n \sum_{j=1}^n w(x_j)} = \sum_{i=1}^n f(x_i) v_i,](images/math/5/f/c/5fc8d6db64d9dbc3f401478d857b5196.png)
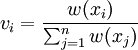 are the normalised importance weights.
are the normalised importance weights.
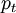 of an event
of an event 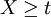 , where
, where 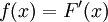 , where prime denotes derivative. A
, where prime denotes derivative. A 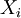 is generated from the distribution
is generated from the distribution 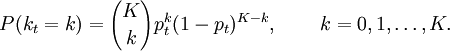
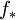 (for X), usually referred to as a biasing density, for the simulation experiment. This density allows the event
(for X), usually referred to as a biasing density, for the simulation experiment. This density allows the event ![p_t = {E} [1(X \ge t)]](images/math/b/1/7/b1729d916d417b534ab6ae97f8f19162.png)
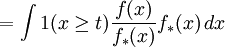
![= {E_*} [1(X \ge t) W(X)]](images/math/6/9/7/697a2c23df5bfcab9895eae30bb8422a.png)
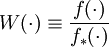
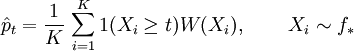
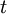 , the estimate is incremented by the weight
, the estimate is incremented by the weight 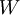 evaluated at the sample value. The results are averaged over
evaluated at the sample value. The results are averaged over  trials. The variance of the IS estimator is easily shown to be
trials. The variance of the IS estimator is easily shown to be
![var_*\hat p_t = \frac{1}{K} var_* [1(X \ge t)W(X)]](images/math/1/d/1/1d173a9895f109d4d20a2972529112c0.png)
![= \frac{1}{K}\Big[{E_*}[1(X \ge t)^2 W^2(X)] - p_t^2 \Big]](images/math/5/0/9/509069cfd8cfc89ed7d11e76cac9270d.png)
![= \frac{1}{K}\Big[{E}[1(X \ge t)^2 W(X)] - p_t^2 \Big]](images/math/4/b/c/4bc30cd7b1f65ad5d6fbfc509dab8784.png)
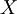 with a number greater than unity has the effect of increasing the variance (mean also) of the density function. This results in a heavier tail of the density, leading to an increase in the event probability. Scaling is probably one of the earliest biasing methods known and has been extensively used in practice. It is simple to implement and usually provides conservative simulation gains as compared to other methods.
with a number greater than unity has the effect of increasing the variance (mean also) of the density function. This results in a heavier tail of the density, leading to an increase in the event probability. Scaling is probably one of the earliest biasing methods known and has been extensively used in practice. It is simple to implement and usually provides conservative simulation gains as compared to other methods.
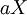 , where usually
, where usually 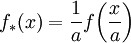
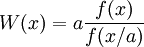
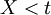 which is undesirable. If
which is undesirable. If 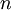 random variables, the spreading of mass takes place in an
random variables, the spreading of mass takes place in an 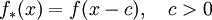
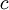 is the amount of shift and is to be chosen to minimize the variance of the IS estimator.
is the amount of shift and is to be chosen to minimize the variance of the IS estimator.
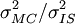 , and this can be interpreted as the speed-up factor by which the IS estimator achieves the same precision as the MC estimator. This has to be computed empirically since the estimator variances are not likely to be analytically possible when their mean is intractable. Other useful concepts in quantifying an IS estimator are the variance bounds and the notion of asymptotic efficiency.
, and this can be interpreted as the speed-up factor by which the IS estimator achieves the same precision as the MC estimator. This has to be computed empirically since the estimator variances are not likely to be analytically possible when their mean is intractable. Other useful concepts in quantifying an IS estimator are the variance bounds and the notion of asymptotic efficiency.


