To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Infrared fixed pointIn physics, an infrared fixed point is a set of coupling constants, or other parameters that evolve from initial values at very high energies (short distance), to fixed stable values, usually predictable, at low energies (large distance). This usually involves the use of the renormalization group, a mathematical apparatus for theoretically evolving physical systems from one scale to another. Product highlightConversely, if the length-scale decreases and the physical parameters approach fixed values, then we have ultraviolet fixed points. The fixed points are generally independent of the initial values of the parameters over a large range of the initial values. This is known as "universality." Statistical PhysicsIn the statistical physics of second order phase transitions, the physical system approaches an infrared fixed point that is independent of the initial short distance dynamics that defines the material. This determines the properties of the phase transition at the critical temperature, or critical point. Observables, such as "critical exponents" usually depend only upon dimension of space, and are independent of the atomic or molecular constituents. Particle PhysicsIn particle physics the best known fixed point is the approach of the strong interaction QCD coupling constant to zero as the energy increases. This an ultraviolet fixed point, associated with the phenomenon known as asymptotic freedom. This causes quarks and gluons to behave as effectively free, or noninteracting, particles at high energies. This phenomenon was first anticipated by "Bjorken Scaling," and observed in electroproduction experiments, and was critical to the development of the theory of strong interactions known as Quantum Chromodynamics. There is a remarkable infrared fixed point of the coupling constants that determine the masses of very heavy quarks. In the Standard Model, quarks and leptons have "Yukawa couplings" to the Higgs boson. These determine the mass of the particle. All of the quark and lepton Yukawa couplings are small compared to the top quark Yukawa coupling. Yukawa couplings are not constants and their properties change depending on the energy scale at which they are measured. The dynamics of Yukawa couplings are determined by the renormalization group equation:
where g3 is the color gauge coupling (which is a function of μ and associated with asymptotic freedom) and y is the Yukawa coupling. This equation describes how the Yukawa coupling changes with energy scale μ. The Yukawa couplings of the up, down, charm, strange and beauty quarks, are small at the extremely
high energy scale of grand unification, On the other hand, solutions to this equation for large initial values y cause the rhs to quickly approach zero. This locks y to the QCD coupling g3. This is known as a (quasi-infrared) fixed point of the renormalization group equation for the Yukawa coupling. No matter what the initial starting value of the coupling is, if it is sufficiently large it will reach this fixed point value, and the corresponding quark mass is predicted. The value of the fixed point is fairly precisely determined in the Standard Model, leading to a predicted top quark mass of 230 GeV. If there is more than one Higgs doublet, the value will be reduced by Higgs mixing angle effects. The observed top quark mass is slightly lower, about 171 GeV (see Top quark). In the minimal supersymmetric extension of the Standard Model (the MSSM), there are two Higgs doublets and the renormalization group equation for the top quark Yukawa coupling is slightly modified. This leads to a fixed point where the top mass is smaller, 170–200 GeV. Some theorists believe this is supporting evidence for the MSSM. The "quasi-infrared fixed point" was proposed in 1981 by C. T. Hill, building on earlier work of B. Pendleton and G. G. Ross. The prevailing view at the time was that the top quark mass would lie in a range of 15 to 26 GeV. The quasi-infrared fixed point has formed the basis of top quark condensation theories of electroweak symmetry breaking in which the Higgs boson is composite at extremely short distance scales, composed of a pair of top and anti-top quarks. Many authors have explored other aspects of infrared fixed points to understand the anticipated spectrum of Higgs bosons in multi-Higgs models. Another example of an infrared fixed point is the Banks-Zaks fixed point in which the coupling constant of a Yang-Mills theory evolves to a fixed large value. The beta-function vanishes, and the theory possesses a symmetry known as "conformal invariance." See also
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Infrared_fixed_point". A list of authors is available in Wikipedia. |





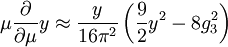 ,
,
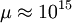 GeV. The
GeV. The 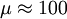 GeV.
GeV.


