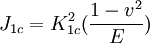My watch list

J integral

The J-integral represents a way to calculate work (energy) per unit fracture surface area in a material.^[1] $J 1 c$ defines the point at which large-scale plastic yielding during propagation takes place under mode one loading.^[1] This value is difficult to determine experimentally, however in 1968 Jim Rice developed the J-integral test that allows one to calculate fracture toughness (K_1c) for materials in which sample sizes are too small (on the order of < 1 meter) for direct determination of K_1c. Physically the J-integral is related to the area under curve of a load versus load point displacement.^[2].

Additional recommended knowledge

J-Integral and Fracture Toughness

The J-integral can be described as follows^[1]

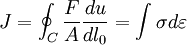
$J=\oint_{C} \frac {F}{A}\frac{du}{dl_0}=\int_{}^{}\sigma d\varepsilon\,$

where

F is the force applied at the crack tip
A is the area of the crack tip
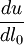$\frac{du}{dl_0}$ is the change in energy per unit length
$σ$ is the stress
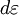$d\varepsilon$ is the change in the strain caused by the stress

Fracture toughness is then calculated from the following equation^[1]

$J_{1c} = K_{1c}^2(\frac{1-v^2}{E})$

where

$K 1 c$ is the fracture toughness in mode one loading
v is the Poisson's ratio
E is the Young's Modulus of the material

References

^ ^a ^b ^c ^d Van Vliet, Krystyn J. (2006); "3.032 Mechanical Behavior of Materials", [1]
^ Meyers and Chawla (1999): "Mechanical Behavior of Materials," 445-448.