To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Fracture toughnessIn materials science, fracture toughness is a property which describes the ability of a material containing a crack to resist fracture, and is one of the most important properties of any material for virtually all design applications.
It is denoted KIc and has the units of The subscript 'Ic' denotes mode I crack opening under a normal tensile stress perpendicular to the crack, since the material can be made thick enough to resist shear (mode II) or tear (mode III). Fracture toughness is a quantitative way of expressing a material's resistance to brittle fracture when a crack is present. If a material has a large value of fracture toughness it will probably undergo ductile fracture. Brittle fracture is very characteristic of materials with a low fracture toughness value. Fracture mechanics, which leads to the concept of fracture toughness, was largely based on the work of A. A. Griffith who, amongst other things, studied the behaviour of cracks in brittle materials. Product highlight
Table of valuesHere are some typical values of fracture toughness for various materials:
Crack Growth as a Stability ProblemConsider a body with flaws (cracks) that is subject to some loading; the stability of the crack can be assessed as follows. We can assume for simplicity that the loading is of constant displacement or displacement controlled type (like loading with a screw jack); we can also simplify the discussion by characterizing the crack by its area A. If we consider an adjacent state of the body as being one with a larger crack (area A+dA), we can then assess the strain energy in the two states and evaluate the strain energy release rate. The rate is reckoned with respect to the change in crack area, so if we use U for strain energy, the strain energy release rate is numerically dU/dA. It may be noted that for a body loaded in constant displacement mode, the displacement is applied and the force level is dictated by the stiffness (or compliance) of the body. If the crack grows in size, the stiffness decreases, so the force level will decrease. this decrease in force level under the same displacement (strain) level indicates that the elastic strain energy stored in the body is decreasing - is being released. Hence the term strain energy release rate which is usually denoted with symbol G. The strain energy release rate is higher for higher loads and larger cracks. If the strain energy so released exceeds a critical value Gc, then the crack will grow spontaneously. For brittle materials, Gc can be equated to the surface energy of the (two) new crack surfaces; in other words, in brittle materials, a crack will grow spontaneously if the strain energy released is equal to or greater than the energy required to grow the crack surface(s). The stability condition can be written as
If the elastic energy releases is less than the critical value, then the crack will not grow; equality signifies neutral stability and if the strain energy release rate exceeds the critical value, the crack will start growing in an unstable manner. For ductile materials, energy associated with plastic deformations has to be taken into account. When there is plastic deformation at the crack tip (as occurs most often in metals) the energy to propagate the crack may increase by several orders of magnitude as the work related to plastic deformation may be much larger than the surface energy. In such cases, the stability criterion has to restated as
Practically, this means a higher value for the critical value Gc. From the definition of G, we can deduce that it has dimensions of work (or energy)/area or force/length. For ductile metals GIc is around 50 to 200 kJ/m2, for brittle metals it is usually 1-5 and for glasses and brittle polymers it is almost always less than 0.5. The I subscript here refers to mode I or crack opening mode as described in the section on fracture mechanics. The problem can also be formulated in terms of stress instead of energy, leading to the terms stress intensity factor K (or KI for mode I) and critical stress intensity factorKc (and KIc). These Kc and KIc (etc) quantities are commonly referred to as fracture toughness, though it is equivalent to use Gc. Typical values for KIcare 150 MN/m3/2 for ductile (very tough) metals, 25 for brittle ones and 1-10 for glasses and brittle polymers. Notice the different units used by GIc and KIc. Engineers tend to use the latter as an indication of toughness. Conjoint ActionThere are number of instances where this picture of a critical crack is modified by corrosion. Thus, fretting corrosion occurs when a corrosive medium is present at the interface between two rubbing surfaces. Fretting (in the absence of corrosion) results from the disruption of very small areas that bond and break as the surfaces undergo friction, often under vibrating conditions. The bonding contact areas deform under the localised pressure and the two surfaces gradually wear away. Fracture mechanics dictates that each minute localised fracture has to satisfy the general rule that the elastic energy released as the bond fractures has to exceed the work done in plastically deforming it and in creating the (very tiny) fracture surfaces. This process is enhanced when corrosion is present, not least because the corrosion products act as an abrasive between the rubbing surfaces. Fatigue is another instance where cyclical stressing, this time of a bulk lump of metal, causes small flaws to develop. Ultimately one such flaw exceeds the critical condition and fracture propagates across the whole structure. The 'fatigue life' of a component is the time it takes for criticality to be reached, for a given regime of cyclical stress. Corrosion fatigue is what happens when a cyclically stressed structure is subjected to a corrosive environment at the same time. This not only serves to initiate surface cracks but (see below) actually modifies the crack growth process. As a result the fatigue life is shortened, often considerably. Stress-Corrosion Cracking (SCC)This phenomenon is the unexpected sudden failure of normally ductile metals subjected to a constant tensile stress in a corrosive environment. Certain austenitic stainless steels and aluminium alloys crack in the presence of chlorides, mild steel cracks in the present of alkali (boiler cracking) and copper alloys crack in ammoniacal solutions (season cracking). Worse still, high-tensile structural steels crack in an unexpectedly brittle manner in a whole variety of aqueous environments, especially chloride. With the possible exception of the latter, which is a special example of hydrogen cracking, all the others display the phenomenon of subcritical crack growth, i.e. small surface flaws propagate (usually smoothly) under conditions where fracture mechanics predicts that failure should not occur. That is, in the presence of a corrodent, cracks develop and propagate well below KIc. In fact, the subcritical value of the stress intensity, designated as KIscc, may be less than 1% of KIc, as the following table shows:
The subcritical nature of propagation may be attributed to the chemical energy released as the crack propagates. That is,
The crack initiates at KIscc and thereafter propagates at a rate governed by the slowest process, which most of the time is the rate at which corrosive ions can diffuse to the crack tip. As the crack advances so K rises (because crack length appears in the calculation of stress intensity). Finally it reaches KIc , whereupon fast fracture ensues and the component fails. One of the practical difficulties with SCC is its unexpected nature. Stainless steels, for example, are employed because under most conditions they are 'passive', i.e. effectively inert. Very often one finds a single crack has propagated while the rest of the metal surface stays apparently unaffected. See also
References
Categories: Continuum mechanics | Materials science |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Fracture_toughness". A list of authors is available in Wikipedia. | |||||||||||||||||||||||||||||||||||||||||||||||||||||


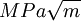 .
.





