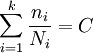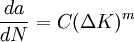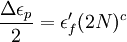In materials science, fatigue is the progressive and localised structural damage that occurs when a material is subjected to cyclic loading. The maximum stress values are less than the ultimate tensile stress limit, and may be below the yield stress limit of the material.
Characteristics of fatigue failures
- The process starts with dislocation movements, eventually forming persistent slip bands that nucleate short cracks.
- Fatigue is a stochastic process, often showing considerable scatter even in controlled environments.
- The greater the applied stress, the shorter the life.
- Fatigue life scatter tends to increase for longer fatigue lives.
- Damage is cumulative. Materials do not recover when rested.
- Fatigue life is influenced by a variety of factors, such as temperature, surface finish, presence of oxidizing or inert chemicals, residual stresses, contact (fretting), etc.
- Some materials (e.g., some steel and titanium alloys) exhibit a theoretical fatigue limit below which continued loading does not lead to failure.
- In recent years, researchers (see for example the work of Bathias, Murakami, and Stanzl-Tschegg) have found that failures occur below the theoretical fatigue limit at very high fatigue lives (109 to 1010 cycles). An ultrasonic resonance technique is used in these experiments with frequencies around 10-20 kHz.
- High cycle fatigue strength (about 103 to 108 cycles) can be described by stress based parameters. A load-controlled, servo-hydraulic test rig is commonly used in these tests, with frequencies of around 20-50 Hz.
- Low cycle fatigue (typically less than 103 cycles) is associated with widespread plasticity, thus a strain based parameter should be used for fatigue life prediction. Testing is conducted with constant strain amplitudes at 1-5 Hz.
Timeline of early fatigue history
- 1837: Wilhelm Albert publishes the first article on fatigue. He devised a test machine for conveyor chains used in the Clausthal mines.[1]
- 1839: Jean-Victor Poncelet describes metals as being tired in his lectures at the military school at Metz.
- 1842: William John Macquorn Rankine[2] recognises the importance of stress concentrations in his investigation of railroad axle failures. The Versailles train crash was caused by axle fatigue.
- 1843: Joseph Glynn reports on fatigue of axle on locomotive tender (see image at right). He identifies the keyway as the crack origin.
- 1848: Railway Inspectorate report one of the first tyre failures, probably from a rivet hole in tread of railway carriage wheel. It was likely a fatigue failure.
- 1849: Eaton Hodgkinson is granted a small sum of money to report to the UK Parliament on his work in ascertaining by direct experiment, the effects of continued changes of load upon iron structures and to what extent they could be loaded without danger to their ultimate security.
- 1854: Braithwaite[3] reports on common service fatigue failures and coins the term fatigue.
- 1860: Systematic fatigue testing undertaken by Sir William Fairbairn and August Wöhler.
- 1870: Wöhler summarises his work on railroad axles. He concludes that cyclic stress range is more important than peak stress and introduces the concept of endurance limit.[1]
- 1903: Sir James Alfred Ewing demonstrates the origin of fatigue failure in microscopic cracks.
- 1910: O. H. Basquin proposes a log-log relationship for SN curves, using Wöhler's test data.
- 1945: A. M. Miner popularises A. Palmgren's (1924) linear damage hypothesis as a practical design tool.
- 1954: L. F. Coffin and S. S. Manson explain fatigue crack-growth in terms of plastic strain in the tip of cracks.
- 1961: P. C. Paris proposes methods for predicting the rate of growth of individual fatigue cracks in the face of initial scepticism and popular defence of Miner's phenomenological approach.
- 1968: Tatsuo Endo and M. Matsuiski devise the rainflow-counting algorithm and enable the reliable application of Miner's rule to random loadings.
- 1970: W. Elber elucidates the mechanisms and importance of crack closure ( more correctly 'non-closure') in slowing the growth of a fatigue crack due to the wedging effect of plastic deformation left behind the tip of the crack.
High-cycle fatigue
Historically, most attention has focused on situations that require more than 104 cycles to failure where stress is low and deformation primarily elastic.
The S-N curve
In high-cycle fatigue situations, materials performance is commonly characterised by an S-N curve, also known as a Wöhler curve. This is a graph of the magnitude of a cyclical stress (S) against the logarithmic scale of cycles to failure (N).
S-N curves are derived from tests on samples of the material to be characterised (often called coupons) where a regular sinusoidal stress is applied by a testing machine which also counts the number of cycles to failure. This process is sometimes known as coupon testing. Each coupon test generates a point on the plot though in some cases there is a runout where the time to failure exceeds that available for the test (see censoring). Analysis of fatigue data requires techniques from statistics, especially survival analysis and linear regression.
Probabilistic nature of fatigue
As coupons sampled from a homogeneous frame will manifest variation in their number of cycles to failure, the S-N curve should more properly be an S-N-P curve capturing the probability of failure after a given number of cycles of a certain stress. Probability distributions that are common in data analysis and in design against fatigue include the lognormal distribution, extreme value distribution and Weibull distribution.
Complex loadings
In practice, a mechanical part is exposed to a complex, often random, sequence of loads, large and small. In order to assess the safe life of such a part:
- Reduce the complex loading to a series of simple cyclic loadings using a technique such as rainflow analysis;
- Create an histogram of cyclic stress from the rainflow analysis;
- For each stress level, calculate the degree of cumulative damage incurred from the S-N curve; and
- Combine the individual contributions using an algorithm such as Miner's rule.
Miner's rule
In 1945, M. A. Miner popularised a rule that had first been proposed by A. Palmgren in 1924. The rule, variously called Miner's rule or the Palmgren-Miner linear damage hypothesis, states that where there are k different stress magnitudes in a spectrum, Si (1 ≤ i ≤ k), each contributing ni(Si) cycles, then if Ni(Si) is the number of cycles to failure of a constant stress reversal Si, failure occurs when:
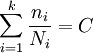
C is experimentally found to be between 0.7 and 2.2. Usually for design purposes, C is assumed to be 1.
This can be thought of as assessing what proportion of life is consumed by stress reversal at each magnitude then forming a linear combination of their aggregate.
Though Miner's rule is a useful approximation in many circumstances, it has two major limitations:
- It fails to recognise the probabilistic nature of fatigue and there is no simple way to relate life predicted by the rule with the characteristics of a probability distribution.
- There is sometimes an effect in the order in which the reversals occur. In some circumstances, cycles of high stress followed by low stress cause more damage than would be predicted by the rule.
Paris' Relationship
Paris derived relationships for the stage II crack growth with cycles N, in terms of the cyclical component ΔK of the Stress Intensity Factor K
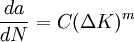
where 2a is the crack length and m is typically in the range 3 to 5.
This relationship was later modified (by Forman, 1967[1]) to make better allowance for the mean stress, by introducing a factor depending on (1-R) where R = min. stress/max stress, in the denominator.
Low-cycle fatigue
Where the stress is high enough for plastic deformation to occur, the account in terms of stress is less useful and the strain in the material offers a simpler description. Low-cycle fatigue is usually characterised by the Coffin-Manson relation (published independently by L. F. Coffin in 1954 and S. S. Manson 1953):
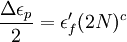
-where:
- Δεp /2 is the plastic strain amplitude;
- εf' is an empirical constant known as the fatigue ductility coefficient, the failure strain for a single reversal;
- 2N is the number of reversals to failure (N cycles);
- c is an empirical constant known as the fatigue ductility exponent, commonly ranging from -0.5 to -0.7 for metals.
A similar relationship for materials such as Zirconium, used in the nuclear industry, is due to W.J. O'Donnell and B. F. Langer (Nuclear Science and Engineering, vol 20, pp 1-12, 1964).
Fatigue and fracture mechanics
The account above is purely phenomenological and, though it allows life prediction and design assurance, it does not enable life improvement or design optimisation. For the latter purposes, an exposition of the causes and processes of fatigue is necessary. Such an explanation is given by fracture mechanics in four stages.
- Crack nucleation;
- Stage I crack-growth;
- Stage II crack-growth; and
- Ultimate ductile failure.
Factors that affect fatigue-life
- Magnitude of stress including stress concentrations caused by part geometry.
- Quality of the surface; surface roughness, scratches, etc. cause stress concentrations or provide crack nucleation sites which can lower fatigue life depending on how the stress is applied. On the other hand, surface stress can be intentionally manipulated to increase fatigue life. For example, shot peening is widely used to put the surface in a state of compressive stress which inhibits surface crack formation and thus improves fatigue life. Such techniques for producing surface stress are often referred to generically as peening, whatever the mechanism used to produce the stress. Other more recently introduced surface treatments, such as laser peening and ultrasonic impact treatment, can also produce this surface compressive stress and can increase the fatigue life of the component. This improvement is normally observed only for high-cycle fatigue. Little improvement is obtained in the low-cycle fatigue régime.
- Material Type. Certain materials, such as steel, will never fail due to fatigue if the stresses remain below a certain level. Other materials, such as aluminum, will eventually fail due to fatigue regardless of the stresses the material sees.
- Surface defect geometry and location. The size, shape, and location of surface defects such as scratches, gouges, and dents can have a significant impact on fatigue life.
- Significantly uneven cooling, leading to a heterogeneous distribution of material properties such as hardness and ductility and, in the case of alloys, structural composition. Uneven cooling of castings, for example, can produce high levels of tensile residual stress, which will encourage crack growth.
- Size, frequency, and location of internal defects. Casting defects such as gas porosity and shrinkage voids, for example, can significantly impact fatigue life.
- In metals where strain-rate sensitivity is observed (ferrous metals, copper, titanium, etc.) strain rate also affects fatigue life in low-cycle fatigue situations.
- For non-isotropic materials, the direction of the applied stress can affect fatigue life.
- Grain size. For most metals, fine-grained parts exhibit a longer fatigue life than coarse-grained parts.
- Environmental conditions and exposure time can cause erosion, corrosion, or gas-phase embrittlement, which all affect fatigue life. Corrosion fatigue is a problem encountered in many aggressive environments.
- The operating temperature over which the part is exposed to affects fatigue life.
Design against fatigue
Dependable design against fatigue-failure requires thorough education and supervised experience in structural engineering, mechanical engineering, or materials science.
There are three principal approaches to life assurance for mechanical parts that display increasing degrees of sophistication:
- Design to keep stress below threshold of fatigue limit (infinite lifetime concept);
- Design (conservatively) for a fixed life after which the user is instructed to replace the part with a new one (a so-called lifed part, finite lifetime concept, or "safe-life" design practice);
- Instruct the user to inspect the part periodically for cracks and to replace the part once a crack exceeds a critical length. This approach usually uses the technologies of nondestructive testing and requires an accurate prediction of the rate of crack-growth between inspections. This is often referred to as damage tolerant design or "retirement-for-cause".
Stopping fatigue
Fatigue cracks that have begun to propagate can sometimes be stopped by drilling holes, called drill stops, in the path of the fatigue crack.[4] However, it is not recommended because a hole represents a stress concentration factor of about 2. There is thus the possibility of a new crack starting in the side of the hole. It is always far better to replace the cracked part entirely. Several disasters have been caused by botched repairs to cracked structures, such as JAL 123.
Material change
Changes in the materials used in parts can also improve fatigue life. Parts can be made from better fatigue rated metals for example. Complete replacement and redesign of parts can also reduce if not eliminate fatigue problems. Thus helicopter rotor blades and propellors in metal are being replaced by composite equivalents. They are not only lighter, but also much more resistant to fatigue. They are more expensive, but the extra cost is amply repaid by their greater integrity, since loss of a rotor blade usually leads to total loss of the aircraft. A similar argument has been made for replacement of metal fuselages, wings and tails of aircraft.
Infamous fatigue failures
Versailles train crash
On May 8, 1842 one of the trains carrying revellers on their return from Versailles to Paris, having witnessed the celebrations of the birthday of Louis Philippe, derailed and caught fire. Though the resulting conflagration mutilated the dead beyond recognition or enumeration, it is estimated that 53 perished and around 40 were seriously injured.
The derailment had been the result of a broken locomotive axle. Rankine's investigation of broken axles in Britain highlighted the importance of stress concentration, and the mechanism of crack growth with repeated loading.
De Havilland Comet
Metal fatigue came strongly to the notice of aircraft engineers in 1954 after three de Havilland Comet passenger jets had broken up in mid-air and crashed within a single year. Investigators from the Royal Aircraft Establishment at Farnborough in England told a public enquiry that the sharp corners around the plane's window openings (actually the forward ADF antenna window in the roof) acted as initiation sites for cracks. The skin of the aircraft was also too thin, and cracks from manufacturing stresses were present at the corners. All aircraft windows were immediately redesigned with rounded corners.
Others
- The Liberty Ships during World War II
- Capsize of the oil platform Alexander Kielland
- United Airlines Flight 232, Japan Airlines Flight 123, China Airlines Flight 611, and Aloha Airlines Flight 243
- The Boston Molasses Disaster has been attributed to a fatigue failure
- The 1998 Eschede train disaster (crash of an InterCityExpress train).
See also
References
- ^ a b W. Schutz (1996). A history of fatigue. Engineering Fracture Mechanics 54: 263-300. DOI
- ^ W.J.M. Rankine. (1842). "On the causes of the unexpected breakage of the journals of railway axles, and on the means of preventing such accidents by observing the law of continuity in their construction". Institution of Civil Engineers, Minutes of Proceedings, 105-108.
- ^ F. Braithwaite. (1854). "On the fatigue and consequent fracture of metals". Institution of Civil Engineers, Minutes of Proceedings, 463–474.
- ^ Material Technologies, Inc. Completes EFS Inspection of Bridge in New Jersey Press release regarding metal fatigue damage to the Manahawkin Bay Bridge in New Jersey
- Andrew, W. (1995) Fatigue and Tribological Properties of Plastics and Elastomers, ISBN 1-884207-15-4
- Dieter, G. E. (1988) Mechanical Metallurgy, ISBN 0-07-100406-8
- Little, R. E. & Jebe, E. H. (1975) Statistical design of fatigue experiments ISBN 0-470-54115-6
|