To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Kaczmarz methodProduct highlight
OverviewThe Kaczmarz method, based on the work of Polish Professor Stefan Kaczmarz, is a method for solving linear systems of equations Ax = b. It is an iterative algorithm that has found many applications ranging from computer tomography to digital signal processing. The method needs, unlike most other linear iterative solvers, not a positive definite but only an invertible matrix A. Therefore it can be used in almost all applications (although most other iterative solvers are for special cases much faster than the Kaczmarz method). Recently, a randomized version of the Kaczmarz method for overdetermined linear systems that converges at an exponential rate was introduced by Thomas Strohmer and Roman Vershynin. This new solver's rate does not depend on the number of equations in the system and outperforms all previously known methods on extremely overdetermined systems. Even for moderately overdetermined systems, numerical simulations reveal that the algorithm can converge faster than the conjugate gradient algorithm. The basic (non randomized) algorithmGiven a full rank real or complex m x n matrix A (n ≤ m) and a real or complex vector b the following iteration computes a better approximation of the equations solution x:
The initial value of x is not important for convergence, although it's better if an appropriate value is chosen. The formulae above gives a simple iteration routine. A complete iteration requires m simple iterations. The new randomized algorithmIt can be shown (see A randomized solver for linear systems with exponential convergence Thomas Strohmer and Roman Vershynin [1]) that the above algorithm runs significantly faster if i is chosen at random (with probability proportional to References
Categories: Radiology | Medical imaging |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Kaczmarz_method". A list of authors is available in Wikipedia. |





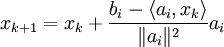 where
where
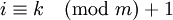
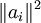 for each simple iteration.
for each simple iteration.


