Laplace principle (large deviations theory)

In mathematics, Laplace's principle is a basic theorem in large deviations theory, similar to Varadhan's lemma. It gives an asymptotic expression for the Lebesgue integral of exp(−θφ(x)) over a fixed set A as θ becomes large. Such expressions can be used, for example, in statistical mechanics to determining the limiting behaviour of a system as the temperature tends to absolute zero.

Additional recommended knowledge

What is the Sensitivity of my Balance?

What is the Correct Way to Check Repeatability in Balances?

Safe Weighing Range Ensures Accurate Results

Statement of the result

Let A be a Lebesgue-measurable subset of d-dimensional Euclidean space R^d and let φ : R^d → R be a measurable function with

$\int_{A} e^{- \varphi(x)} \, \mathrm{d} x < + \infty.$

Then

$\lim_{\theta \to + \infty} \frac1{\theta} \log \int_{A} e^{- \theta \varphi(x)} \, \mathrm{d} x = - \mathop{\mathrm{ess \, inf}}_{x \in A} \varphi(x),$

where ess inf denotes the essential infimum. Heuristically, this may be read as saying that for large θ,

$\int_{A} e^{- \theta \varphi(x)} \, \mathrm{d} x \approx \exp \left( - \theta \mathop{\mathrm{ess \, inf}}_{x \in A} \varphi(x) \right).$

Application

The Laplace principle can be applied to the family of probability measures P_θ given by

$\mathbf{P}_{\theta} (A) = \left( \int_{A} e^{- \theta \varphi(x)} \, \mathrm{d} x \right) \Big/ \left( \int_{\mathbf{R}^{d}} e^{- \theta \varphi(y)} \, \mathrm{d} y \right)$

to give an asymptotic expression for the probability of some set/event A as θ becomes large. For example, if X is a standard normally distributed random variable on R, then

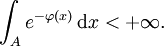
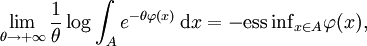
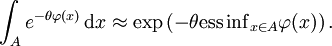
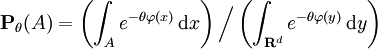
$\lim_{\varepsilon \downarrow 0} \varepsilon \log \mathbf{P} \big[ \sqrt{\varepsilon} X \in A \big] = - \mathop{\mathrm{ess \, inf}}_{x \in A} \frac{x^{2}}{2}$

for every measurable set A.

References

Dembo, Amir; Zeitouni, Ofer (1998). Large deviations techniques and applications, Second edition, Applications of Mathematics (New York) 38, New York: Springer-Verlag, xvi+396. ISBN 0-387-98406-2. MR1619036

Category: Statistical mechanics