To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Recurrence period density entropyIn dynamical systems, stochastic processes, and time series analysis, recurrence period density entropy (RPDE) is a method for determining the periodicity, or repetitiveness of a signal. It is useful for characterising the extent to which a time series repeats the same sequence, and is therefore similar to linear autocorrelation and time delayed mutual information, except that it measures repetitiveness in the phase space of the system, and is thus a more reliable measure based upon the dynamics of the underlying system that generated the signal. It has the advantage that it does not require the assumptions of linearity, Gaussianity or dynamical determinism. It has been successfully used to detect abnormalities in biomedical contexts such as speech and ECG signals (Little et al. 2006, 2007). Product highlightThe RPDE value Method descriptionThe RPDE method first requires the embedding of a time series in phase space, which, according to stochastic extensions to Taken's embedding theorems, can be carried out by forming time-delayed vectors: for each value xn in the time series, where m is the embedding dimension, and τ is the embedding delay. These parameters are obtained by systematic search for the optimal set (due to lack of practical embedding parameter techniques for stochastic systems) (Stark et al. 2003). Next, around each point is the RPDE value, where RPDE in practiceRPDE has the ability to detect subtle changes in natural biological time series such as the breakdown of regular periodic oscillation in abnormal cardiac function which are hard to detect using classical signal processing tools such as the Fourier transform or linear prediction. The recurrence period density is a sparse representation for nonlinear, non-Gaussian and nondeterministic signals, whereas the Fourier transform is only sparse for purely periodic signals. References
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Recurrence_period_density_entropy". A list of authors is available in Wikipedia. |





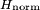 is a scalar in the range zero to one. For purely periodic signals,
is a scalar in the range zero to one. For purely periodic signals, 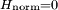 , whereas for purely i.i.d., uniform white noise,
, whereas for purely i.i.d., uniform white noise, 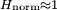 (Little et al. 2007).
(Little et al. 2007).
![\mathbf{X}_n=[x_n, x_{n+\tau}, x_{n+2\tau}, \ldots, x_{n+(m-1)\tau}]](images/math/2/6/0/26094fe3c6b33116c455aa69165f8370.png)
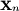 in the phase space, an
in the phase space, an 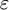 -neighbourhood (an m-dimensional ball with this radius) is formed, and every time the time series returns to this ball, the time difference T between successive returns is recorded in a histogram. This histogram is normalised to sum to unity, to form an estimate of the recurrence period density function P(T). The normalised entropy of this density:
-neighbourhood (an m-dimensional ball with this radius) is formed, and every time the time series returns to this ball, the time difference T between successive returns is recorded in a histogram. This histogram is normalised to sum to unity, to form an estimate of the recurrence period density function P(T). The normalised entropy of this density:
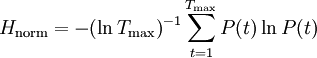
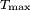 is the largest recurrence value (typically on the order of 1000 samples) (Little et al. 2007).
is the largest recurrence value (typically on the order of 1000 samples) (Little et al. 2007).


