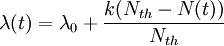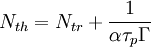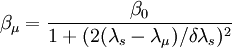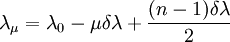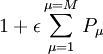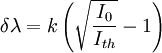To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Laser diode rate equations
The rate equations may be solved by numerical integration to obtain a time-domain solution, or used to derive a set of steady state or small signal equations to help in further understanding the static and dynamic characteristics of semiconductor lasers. The laser diode rate equations can be formulated with more or less complexity to model different aspects of laser diode behavior with varying accuracy. Product highlight
Multimode rate equationsIn the multimode formulation, the rate equations model a laser with multiple optical modes. This formulation requires one equation for the carrier density, and one equation for the photon density in each of the optical cavity modes: where: M is the number of modes modelled, μ is the mode number, and subscript μ has been added to G, Γ, and β to indicate these properties may vary for the different modes. The modal gainGμ, the gain of the μth mode, can be modelled by a parabolic dependence of gain on wavelength as follows: where: α is the gain coefficient and ε is the gain compression factor (see below). λμ is the wavelength of the μth mode, δλg is the full width at half maximum (FWHM) of the gain curve, the centre of which is given by where λ0 is the centre wavelength for N = Nth and k is the spectral shift constant (see below). Nth is the carrier density at threshold and is given by where Ntr is the carrier density at transparency.
where β0 is the spontaneous emission factor, λs is the centre wavelength for spontaneous emission and δλs is the spontaneous emission FWHM. Finally, λμ is the wavelength of the μth mode and is given by where δλ is the mode spacing. Gain CompressionThe gain term, G, cannot be independent of the high power densities found in semiconductor laser diodes. There are several phenomena which cause the gain to 'compress' which are dependent upon optical power. The two main phenomena are spatial hole burning and spectral hole burning. Spatial hole burning occurs as a result of the standing wave nature of the optical modes. Increased lasing power results in decreased carrier diffusion efficiency which means that the stimulated recombination time becomes shorter relative to the carrier diffusion time. Carriers are therefore depleted faster at the crest of the wave causing a decrease in the modal gain. Spectral hole burning is related to the gain profile broadening mechanisms such as short intraband scattering which is related to power density. To account for gain compression due to the high power densities in semiconductor lasers, the gain equation is modified such that it becomes related to the inverse of the optical power. Hence, the following term in the denominator of the gain equation : Spectral ShiftDynamic wavelength shift in semiconductor lasers occurs as a result of the change in refractive index in the active region during intensity modulation. It is possible to evaluate the shift in wavelength by determining the refractive index change of the active region as a result of carrier injection. A complete analysis of spectral shift during direct modulation found that the refractive index of the active region varies proportionally to carrier density and hence the wavelength varies proportionally to injected current. Experimentally, a good fit for the shift in wavelength is given by: where I0 is the injected current and Ith is the lasing threshold current. |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Laser_diode_rate_equations". A list of authors is available in Wikipedia. |





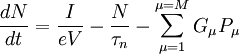
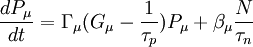
![G_\mu = \frac{\alpha N [1-(2\frac{\lambda(t)-\lambda_\mu}{\delta\lambda_g})^2] - \alpha N_0}{1 + \epsilon \sum_{\mu=1}^{\mu=M}P_\mu}](images/math/6/c/7/6c737b35223ca4f618af8f1c08a36be7.png)