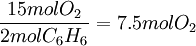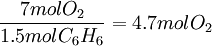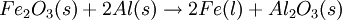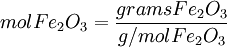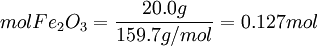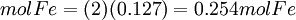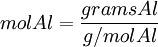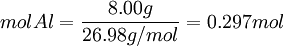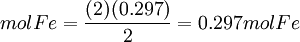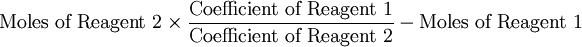To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Limiting reagentIn chemistry, the limiting reagent, or also called the "limiting reactant", is the chemical that determines how far the reaction will go before the chemical in question gets used up, causing the reaction to stop. The chemical of which there are fewer mols than the proportion requires is the limiting reagent. Product highlight
ExampleConsider the combustion of benzene: 1.5 mol C6H6 × This means that 11.25 mol O2 is required to react with 1.5 mol C6H6. Since only 7 mol O2 is present, the oxygen will be consumed before benzene. Therefore, O2 must be the limiting reagent. This conclusion can be verified by comparing the mole ratio of O2 and C6H6 required by the balanced equation with the mole ratio actually present: required: actual: Since the actual ratio is too small, O2 is the limiting reagent. Consider a typical thermite reaction: If 20.0 g of Fe2O3 are reacted with 8.00 g Al(s) in the thermite reaction, Which reactant is limiting?.
First, determine how many moles of Fe(l) can be produced from either reactant. Moles produced of Fe from reactant Fe2O3
Moles produced of Fe from reactant Al
Because the moles Fe produced from Fe2O3(0.254mol) is less than the moles Fe produced from Al(0.297mol), Fe2O3 is the limiting reagent. By looking at chemical equation for the thermite reaction, the limiting reagent can be found based on the ratio of moles of one reactant to another and the total atomic mass of the reactant compounds. Limiting reagent formulaThere is a much simpler formula which can be used. However, you must first calculate the moles of both of the reagents in the reaction. Once the number of moles have been figured out, just simply fill in this equation (Reagent 1 being the first reactant, 2 being the second):
When the answer to the formula is less than zero, reagent 1 is the excess reagent. When the answer is larger than zero, reagent 1 is the limiting reagent. The number shows how much in excess one reagent is from another. If the answer for the formula is zero, both reagents are perfectly balanced. The unit of an answer is in moles. References
See also
Categories: Chemical reactions | Stoichiometry |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Limiting_reagent". A list of authors is available in Wikipedia. |





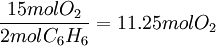
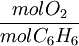 =
=