To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Long Josephson junctionIn superconductivity, a long Josephson junction (LJJ) is a Josephson junction which has one or more dimensions longer than the Josephson penetration depth λJ. This definition is not strict. Product highlightIn terms of underlying model a short Josephson junction is characterized by the Josephson phase φ(t), which is only a function of time, but not of coordinates i.e. the Josephson junction is assumed to be point-like in space. In contrast, in a long Josephson junction the Josephson phase can be a function of one or two spacial coordinates, i.e., φ(x,t) or φ(x,y,t). Simple model: the sine-Gordon equationThe simplest and the most frequently used model which describes the dynamics of the Josephson phase φ in LJJ is the so-called perturbed sine-Gordon equation. For the case of 1D LJJ it looks like: 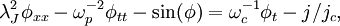 where subscripts x and t denote partial derivatives with respect to x and t, λJ is the Josephson penetration depth, ωp is the Josephson plasma frequency, ωc is the so-called characteristic frequency and j / jc is the bias current density j normalized to the critical current density jc. In the above equation, the r.h.s. is considered as perturbation. Usually for theoretical studies one uses normalized sine-Gordon equation: where spatial coordinate is normalized to the Josephson penetration depth λJ and time is normalized to the inverse plasma frequency Important solutions
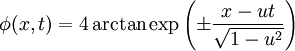 Here x, t and u = v / c0 are the normalized coordinate, normalized time and normalized velocity. The physical velocity v is normalized to the so-called Swihart velocity c0 = λJωp, which represent a typical unit of velocity and equal to the unit of space λJ divided by unit of time Categories: Superconductivity | Josephson effect |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Long_Josephson_junction". A list of authors is available in Wikipedia. |





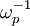 . The parameter
. The parameter 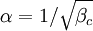 is the dimensionless damping parameter (
is the dimensionless damping parameter (

