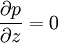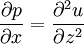To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Lubrication theoryA branch of fluid dynamics, lubrication theory is used to describe the flow of fluids (liquids or gases) in a geometry in which one dimension is significantly smaller than the others. Interior flows are those where the boundaries of the fluid volume are known, and include those inside bearings. Here a key goal of lubrication theory is to determine the pressure distribution in the fluid volume, and hence the forces on the bearing components. The working fluid in this case is often termed a lubricant. Free film lubrication theory is concerned with the case in which one of the surfaces containing the fluid is a free surface. In that case the position of the free surface is itself unknown, and one goal of lubrication theory is then to determine this. Surface tension may then be significant, or even dominant. Issues of wetting and dewetting then arise. For very thin films (thickness less than one micrometre), additional intermolecular forces, such as disjoining forces, may become significant. Product highlight
Theoretical basisMathematically, lubrication theory can be seen as exploiting the disparity between two length scales. The first is the characteristic film thickness, H, and the second is a characteristic substrate length scale L. The key requirement for lubrication theory is that the ratio ε = H / L is small, that is, where x and z are coordinates in the direction of the substrate and perpendicular to it respectively. Here p is the fluid pressure, and u is the fluid velocity component parallel to the substrate. Further details can be found in the literature[1] or in the textbooks given in the bibliography. ApplicationsImportant application areas include lubrication of machinery, fluid bearings, coating (including the preparation of thin films, printing, and painting), and adhesives. Biological applications have included studies of liquid flow in the lung and eye. Notes
References
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Lubrication_theory". A list of authors is available in Wikipedia. |





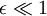 .
The
.
The