To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Magnetic flux quantumThe magnetic flux quantum Φ0 is the quantum of magnetic flux passing through a superconductor. The inverse of the flux quantum, 1/Φ0, is called the Josephson constant, and is denoted KJ. The quantization of magnetic flux is closely related to the Aharonov-Bohm effect, but was predicted earlier by F. London in 1948 using a phenomenological model. Product highlight
IntroductionIt is a property of a supercurrent (superconducting electrical current) that the magnetic flux passing through any area bounded by such a current is quantized. The quantum of magnetic flux is a physical constant, as it is independent of the underlying material as long as it is a superconductor. Its value is The Josephson constantThe Josephson constant is the inverse of the quantum of magnetic flux: If the area under consideration consists entirely of superconducting material, the magnetic flux through it will be zero, for supercurrents always flow in such a way as to expel magnetic fields from the interior of a superconductor, a phenomenon known as the Meissner effect. A non-zero magnetic flux may be obtained by embedding a ring of superconducting material in a normal (non-superconducting) medium. There are no supercurrents present at the center of the ring, so magnetic fields can pass through. However, the supercurrents at the boundary will arrange themselves so that the total magnetic flux through the ring is quantized in units of Φ0. This is the idea behind SQUIDs, which are the most accurate type of magnetometer available. A similar effect occurs when a superconductor is placed in a magnetic field. At sufficiently high field strengths, some of the magnetic field may penetrate the superconductor in the form of thin threads of material that have turned normal. These threads, which are sometimes called fluxons because they carry magnetic flux, are in fact the central regions ("cores") of vortices in the supercurrent. Each fluxon carries an integer number of magnetic flux quanta. Measuring the magnetic fluxThe magnetic flux quantum may be measured with great precision by exploiting the Josephson effect. In fact, when coupled with the measurement of the von Klitzing constant RK = h / e², this provides the most precise values of Planck's constant h obtained to date. This is remarkable since h is generally associated with the behavior of microscopically small systems, whereas the quantization of magnetic flux in a superconductor and the quantum Hall effect are both collective phenomena associated with thermodynamically large numbers of particles. See also: Dirac flux quantum References
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Magnetic_flux_quantum". A list of authors is available in Wikipedia. |





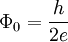 = 2.067 833 636×10−15
= 2.067 833 636×10−15 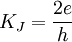 = 483 597.9×109
= 483 597.9×109 

