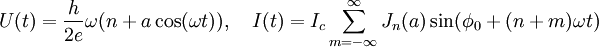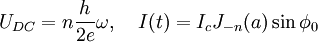The Josephson effect is the phenomenon of current flow across two weakly coupled superconductors, separated by a very thin insulating barrier. This arrangement—two superconductors linked by a non-conducting barrier—is known as a Josephson junction; the current that crosses the barrier is the Josephson current. The terms are named after British physicist Brian David Josephson, who predicted the existence of the effect in 1962[1]. It has important applications in quantum-mechanical circuits, such as SQUIDs.
The effect
The basic equations [2] governing the dynamics of the Josephson effect are
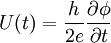 (superconducting phase evolution equation) (superconducting phase evolution equation)
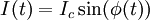 (Josephson or weak-link current-phase relation) (Josephson or weak-link current-phase relation)
where 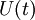 and and 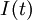 are the voltage and current across the Josephson junction, are the voltage and current across the Josephson junction, 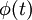 is the "phase difference" across the junction (i.e., the difference in phase factor, or equivalently, argument, between the Ginzburg-Landau complex order parameter of the two superconductors comprising the junction), and is the "phase difference" across the junction (i.e., the difference in phase factor, or equivalently, argument, between the Ginzburg-Landau complex order parameter of the two superconductors comprising the junction), and 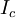 is a constant, the critical current of the junction. The critical current is an important phenomenological parameter of the device that can be affected by temperature as well as by an applied magnetic field. The physical constant, is a constant, the critical current of the junction. The critical current is an important phenomenological parameter of the device that can be affected by temperature as well as by an applied magnetic field. The physical constant, 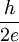 is the magnetic flux quantum, the inverse of which is the Josephson constant. is the magnetic flux quantum, the inverse of which is the Josephson constant.
The three main effects predicted by Josephson follow from these relations:
- The DC Josephson effect. This refers to the phenomenon of a direct current crossing the insulator in the absence of any external electromagnetic field, owing to tunneling. This DC Josephson current is proportional to the sine of the phase difference across the insulator, and may take values between
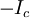 and and 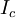 . .
- The AC Josephson effect. With a fixed voltage
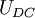 across the junctions, the phase will vary linearly with time and the current will be an AC current with amplitude across the junctions, the phase will vary linearly with time and the current will be an AC current with amplitude 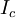 and frequency and frequency 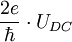 . The complete expression for the current drive Iext becomes . The complete expression for the current drive Iext becomes 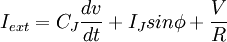 . This means a Josephson junction can act as a perfect voltage-to-frequency converter. . This means a Josephson junction can act as a perfect voltage-to-frequency converter.
- The inverse AC Josephson effect. If the phase takes the form
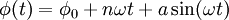 , the voltage and current will be , the voltage and current will be
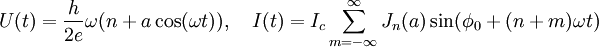 The DC components will then be
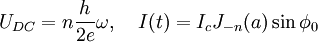 Hence, for distinct DC voltages, the junction may carry a DC current and the junction acts like a perfect frequency-to-voltage converter.
Applications
The Josephson effect has found wide usage, for example in the following areas:
- SQUIDs, or superconducting quantum interference devices, are very sensitive magnetometers that operate via the Josephson effect. They are widely used in science and engineering. (See main article: SQUID.)
- In precision metrology, the Josephson effect provides an exactly reproducible conversion between frequency and voltage. Since the frequency is already defined precisely and practically by the caesium standard, the Josephson effect is used, for most practical purposes, to give the definition of a volt (although, as of July 2007, this is not the official BIPM definition [1]).
- Single-electron transistors are often constructed of superconducting materials, allowing use to be made of the Josephson effect to achieve novel effects. The resulting device is called a "superconducting single-electron transistor"[3].
See also
- [[Josephson junction] http://en.wiktionary.org/wiki/Josephson_junction]
- Josephson diode
- Peptide molecular photodiode
References
- ^ B. D. Josephson. The discovery of tunnelling supercurrents. Rev. Mod. Phys. 1974; 46(2): 251-254.
- ^ Barone A, Paterno G. Physics and Applications of the Josephson Effect. New York: John Wiley & Sons; 1982.
- ^ Fulton, T.A.; et al. (1989). "Observation of Combined Josephson and Charging Effects in Small Tunnel Junction Circuits". Physical Review Letters 63 (12): 1307-1310.
|





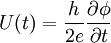 (superconducting phase evolution equation)
(superconducting phase evolution equation)
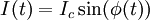 (Josephson or weak-link current-phase relation)
(Josephson or weak-link current-phase relation)
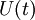 and
and 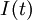 are the voltage and current across the Josephson junction,
are the voltage and current across the Josephson junction, 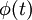 is the "phase difference" across the junction (i.e., the difference in phase factor, or equivalently, argument, between the
is the "phase difference" across the junction (i.e., the difference in phase factor, or equivalently, argument, between the 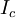 is a constant, the critical current of the junction. The critical current is an important phenomenological parameter of the device that can be affected by temperature as well as by an applied magnetic field. The physical constant,
is a constant, the critical current of the junction. The critical current is an important phenomenological parameter of the device that can be affected by temperature as well as by an applied magnetic field. The physical constant, 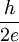 is the
is the 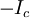 and
and 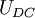 across the junctions, the phase will vary linearly with time and the current will be an AC current with amplitude
across the junctions, the phase will vary linearly with time and the current will be an AC current with amplitude 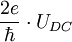 . The complete expression for the current drive
. The complete expression for the current drive 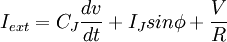 . This means a Josephson junction can act as a perfect voltage-to-frequency converter.
. This means a Josephson junction can act as a perfect voltage-to-frequency converter.
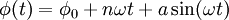 , the voltage and current will be
, the voltage and current will be